题目内容
某工厂某种产品的年固定成本为250万元,每生产 千件,需另投入成本为
千件,需另投入成本为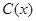 ,当年产量不足80千件时,
,当年产量不足80千件时, (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时, (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
(1)
(2)当产量为100千件时,该厂在这一商品中所获利润最大,最大利润为1000万元
解析试题分析:(1)根据年利润=销售额-投入的总成本-固定成本,分0<x<80和当x≥80两种情况得到L与x的分段函数关系式;(2)当0<x<80时根据二次函数求最大值的方法来求L的最大值,当x≥80时,利用基本不等式来求L的最大值,最后综合即可.
试题解析:(1)因为每件商品售价为0.05万元,则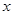 千件商品销售额为0.05×1000
千件商品销售额为0.05×1000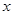 万元,依题意得:
万元,依题意得:
当 时,
时,
 . 2分
. 2分
当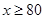 时,
时,
=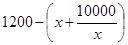 . 4分
. 4分
所以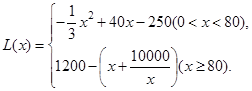 6分
6分
(2)当 时,
时,
此时,当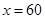 时,
时, 取得最大值
取得最大值 万元. 8分
万元. 8分
当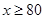 时,
时, 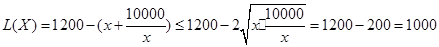
当 时,即
时,即 时
时 取得最大值1000万元. 11分
取得最大值1000万元. 11分
所以,当产量为100千件时,该厂在这一商品中所获利润最大,最大利润为1000万元. 12分
考点:1.分段函数的值域的求法;2.二次函数的最值求法;3.函数模型的应用

练习册系列答案
相关题目
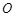 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点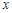 米,圆心角为
米,圆心角为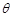 (弧度).
(弧度).
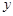 ,求
,求 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式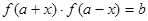 对定义域中的每一个
对定义域中的每一个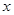 都成立,则称函数
都成立,则称函数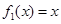 是否为 “(
是否为 “(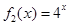 是“(
是“(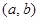 ;,
;, 是“(
是“(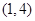 .当
.当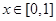 时,
时,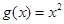
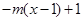
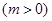 ,若当
,若当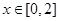 时,都有
时,都有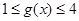 ,试求
,试求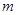 的取值范围.
的取值范围.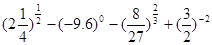 ;⑵
;⑵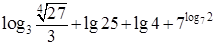 .
.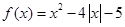 .
.
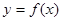 的图象;
的图象;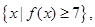 求集合A;
求集合A;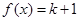 有两解,求实数
有两解,求实数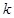 的取值范围.
的取值范围.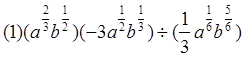
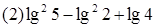
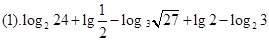
 (m∈N+)的图象关于y轴对称,且在(0,+∞)上是减函数,求满足
(m∈N+)的图象关于y轴对称,且在(0,+∞)上是减函数,求满足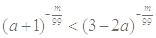 的a的取值范围.
的a的取值范围.