题目内容
已知
=（1，x，x+1），
=（x，4，y），
∥
，则y=
| a |
| b |
| a |
| b |
2或6
2或6
．分析：由条件利用两个向量共线的性质可得
=
=
，由此求得y的值．
| 1 |
| x |
| x |
| 4 |
| x+1 |
| y |
解答：解：∵已知
=（1，x，x+1），
=（x，4，y），
∥
，则得
=
=
，解得
，或
，
故y=2或6，
故答案为 2或6．
| a |
| b |
| a |
| b |
| 1 |
| x |
| x |
| 4 |
| x+1 |
| y |
|
|
故y=2或6，
故答案为 2或6．
点评：本题主要考查两个向量共线的性质，属于基础题．
练习册系列答案
相关题目
已知A={x|-1＜x＜2}，B={x|2x＞1}
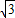sinωx）（其中0＜ω＜1），函数f（x）=a•b，若直线x=
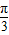是函数f（x）图象的一条对称轴，
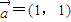，令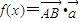
．
；
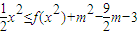都恒成立，求实数m的取值范围．