Question

若函数y=f(x)满足:对任意x、y∈R,f(x+y)=f(x)·f(y)且f(1)=2.

(1)求f(8)的值;

(2)求的值;

(3)求f(n)的表达式(n∈N^*),并求f(1)+f(2)+…+f(n)的值.

Answer 1

解:(1)∵f(x+y)=f(x)·f(y)且f(1)=2,

∴f(8)=f(4+4)=f²(4)=f⁴(2)=f⁸(1)=2⁸=256.

(2)∵f(x+1)=f(x)·f(1),∴=f(1)=2.

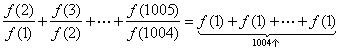∴=2 008.

(3)f(n)=f［(_n-1)+1］=f(_n-1)·f(1)=f(n-2)·f²(1)=…=fⁿ(1)=2ⁿ,

令S=f(1)+f(2)+…+f(n)=2+2²+…+2ⁿ,①

∴2S=2²+2³+…+2ⁿ⁺¹.②

②-①得S=2ⁿ⁺¹-2.(也可由①式直接求和).