Question

[理]已知A、B是抛物线y²=4x上两点，且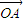•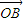=0，则原点O到直线AB的最大距离为（ ）
A．2
B．3
C．4
D．8

Answer 1

【答案】分析：设直线AB的方程为x=my+b，代入抛物线方程消去x，求得y₁+y₁．设A（x₁，y₁），B（x₂，y₂），由•=x₁x₂+y₁y₂整理可得（m²+1）（-4b）+4m²b+b²=b²-4b=0，求得b的值，再根据原点到直线AB的距离为判断当m=0时距离最大，进而求得答案．
解答：解：设直线AB的方程为x=my+b，代入抛物线方程可得y²-4my-4b=0，设A（x₁，y₁），B（x₂，y₂），
由•=x₁x₂+y₁y₂=（my₁+b）（my₂+b）+y₁y₂=（m²+1）y₁y₂+mb（y₁+y₂）+b²=（m²+1）（-4b）+4m²b+b²=b²-4b=0，
解之得b=4或b=0（舍去），
即直线AB的方程为x=my+4，原点到直线AB的距离为d=，
当m=0时，d_最大值=4．
故选C
点评：本题主要考查了抛物线的性质．当直线与抛物线联立时，注意用好韦达定理．