题目内容
(本小题满分12分)
定义在R上的函数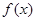 ,
,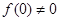 ,当
,当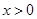 时,
时,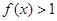 ,且对任意实数
,且对任意实数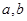 ,
,
有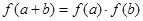 ,
,
(1) 求证: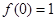 ; (2)求证:对任意的
; (2)求证:对任意的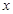 ∈R,恒有
∈R,恒有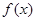 >0;
>0;
(3)证明: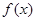 是R上的增函数;(4)若
是R上的增函数;(4)若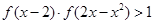 ,求
,求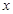 的取值范围.、
的取值范围.、
【答案】
见解析。
【解析】(1)令a=b=0,可知 ,因为
,因为 ,所以f(0)=1.
,所以f(0)=1.
(2)令a=x,b=-x,可得f(0)=f(x)f(-x),再结合f(0)=1,x>0,f(x)>1,可确定当x<0时,f(x)>0,又因为f(0)=1.,从而问题得证.
(3)任取x2>x1,则 ,从而证得结论.
,从而证得结论.
(4) ,
,
从而再利用(3)的单调性转化为不等式 ,从而问题易解.
,从而问题易解.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目