题目内容
定义在 上的函数
上的函数 同时满足以下条件:
同时满足以下条件:
①  在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;
②  是偶函数;③
是偶函数;③ 在
在 处的切线与直线
处的切线与直线 垂直.
垂直.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)设 ,求函数
,求函数 在
在 (
( )上的最小值.
)上的最小值.
解:(Ⅰ) ……………………1分
……………………1分
由已知得 ,即
,即 ,……………………3分
,……………………3分
解得 。……………………5分
。……………………5分
故函数 的解析式为
的解析式为 ……………………5分
……………………5分
(Ⅱ)∵ ,……………………6分
,……………………6分
∴ ………………………………7分
………………………………7分
令 得
得 ,当
,当 时,
时, ,函数
,函数 单调递减;当
单调递减;当 时,
时, ,函数
,函数 单调递增。……………………8分
单调递增。……………………8分
若 ,在
,在 上函数
上函数 单调递增,
单调递增,
此时 ;…………………………………9分
;…………………………………9分
若 ,函数
,函数 在
在 上单调递减,在
上单调递减,在 上单调递减,此时
上单调递减,此时 ;………………………………11分
;………………………………11分
综上可知,函数 在
在 上的最小值为:
上的最小值为:
当 时,
时,
当 时,
时,  .…………………………12分
.…………………………12分

练习册系列答案
相关题目
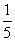 ,则实数t的值为( ).
,则实数t的值为( ).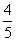 D.
D. 的离心率等于
的离心率等于 ,则m= .
,则m= . ,
, ,给出下列三个结论:
,给出下列三个结论: ,②
,②  , ③
, ③  ,
, 则
则 .
. 
 时,则下列大小关系正确的是
时,则下列大小关系正确的是  B.
B.
 D.
D.
 在区间
在区间 上有两个零点,则
上有两个零点,则 的取值范围是( )
的取值范围是( )



 85,乙班学生成绩的平均分为81,则x+y的值为
85,乙班学生成绩的平均分为81,则x+y的值为 、
、 ,且
,且 是
是 与
与 的等差中项,则动点
的等差中项,则动点 的轨迹方程是 ( )
的轨迹方程是 ( )  B.
B. C.
C. D.
D.