题目内容
已知向量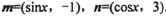 .
.
(I )当m//n时,求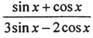 的值;
的值;
(II)已知在锐角ΔABC中,a, b, c分别为角A,B,C的对边,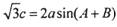 ,函数
,函数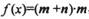 ,求
,求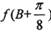 的取值范围
的取值范围
【答案】
(1)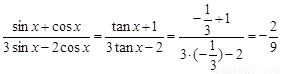
(2)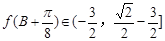
【解析】(I )根据m//n,求得tanx=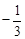 ,然后把所求的式子用tanx表示;(II) 由
,然后把所求的式子用tanx表示;(II) 由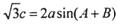 根据正弦定理求得
根据正弦定理求得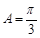 ,求出
,求出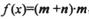 的函数关系式,根据又△ABC为锐角三角形,求得角B的范围,然后求函数的取值范围。
的函数关系式,根据又△ABC为锐角三角形,求得角B的范围,然后求函数的取值范围。
解:(I)由m//n,可得3sinx=-cosx,于是tanx=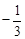 .
.
∴
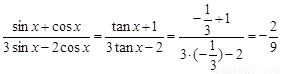 . …………………………4分
. …………………………4分
(II)∵在△ABC中,A+B=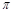 -C,于是
-C,于是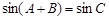 ,
,
由正弦定理知: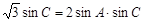 ,
,
∴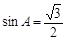 ,可解得
,可解得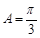 . ………………………………………………6分
. ………………………………………………6分
又△ABC为锐角三角形,于是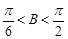 ,
,
∵
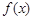 =(m+n)·n
=(m+n)·n
=(sinx+cosx,2)·(sinx,-1)
=sin2x+sinxcosx-2
=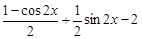
=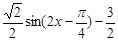 ,
,
∴
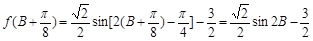 .……………………10分
.……………………10分
由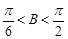 得
得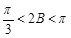 ,
,
∴ 0<sin2B≤1,得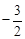 <
<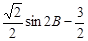 ≤
≤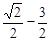 .
.
即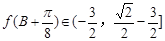 .
.

练习册系列答案
相关题目
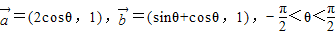
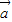 ∥
∥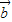 ,求θ的值
,求θ的值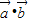 ,求函数f(θ)的最大值及单调递增区间.
,求函数f(θ)的最大值及单调递增区间. (I)若
(I)若 求
求 (II)求
(II)求 的最大值。
的最大值。 (I)若
(I)若 求
求 (II)求
(II)求 的最大值。
的最大值。
 ,求实数
,求实数 的值.
的值.  ,①求
,①求 的所有对称轴方程.②求
的所有对称轴方程.②求 上的单调增区间.
上的单调增区间.