题目内容

13．盒子里有大小一样的15个球，其中10个红球，5个白球，甲、乙两人依次摸一个球，求甲得红球，乙得白球的概率．

分析 甲、乙两人依次摸一个球，有15×14=210种方法，甲得红球，乙得白球有10×5=50种方法，即可得出所求概率．

解答 解：甲、乙两人依次摸一个球，有15×14=210种方法，甲得红球，乙得白球有10×5=50种方法，
所以所求概率为$\frac{5}{21}$．

点评 本题以概率问题为载体，主要考查古典概型，比较基础．

练习册系列答案
相关题目
3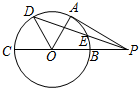．如图，PA切圆O于点A，割线PBC经过圆心O，若PB=OB=1，OD平分∠AOC，交圆O于点D，连接PD交圆O于点E，则PE的长等于（　　）
A．$\frac{{\sqrt{7}}}{7}$B．$\frac{{3\sqrt{7}}}{7}$C．$\frac{{5\sqrt{7}}}{7}$D．$\sqrt{7}$
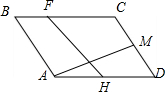4．如图，平行四边形ABCD中，$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，H、M是AD、DC的中点，BF=$\frac{1}{3}$BC．
（1）用$\overrightarrow{a}$，$\overrightarrow{b}$来表示$\overrightarrow{AM}$，$\overrightarrow{HF}$；
（2）若|$\overrightarrow{a}$|=3，|$\overrightarrow{b}$|=4，$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{2π}{3}$，求$\overrightarrow{AM}$•$\overrightarrow{HF}$．
1．已知正项递增的等比数列{an}中，a1=1，2a3与$\frac{3}{2}$a5的等差中项为2a4，数列{bn}的前n项和为Sn满足Sn=$\frac{n{b}_{n}}{2}$，且b2=1．
（1）求数列{an}，{bn}的通项公式；
（2）求数列{$\frac{1}{{a}_{n}}$+$\frac{1}{{S}_{n+1}}$}的前n项和Tn．
8．已知函数f（x）=mx3+3（m-1）x2-m2+1（m＞0）的单调减区间是（0，4），则m=$\frac{1}{3}$．
18．函数f（x）=$\frac{（{4}^{x}+1）}{（{2}^{x}-\frac{4}{3}）•{2}^{x}}$-a有且只有一个零点，则a的范围为（　　）
A．a＞1B．a＞1或a=-3C．0＜a＜1或a=-3D．a＞-1
7．若$\frac{1}{tanα-1}$无意义，则α在[0，π]内的值是$\frac{π}{4}$或$\frac{π}{2}$．
4．已知函数f（x）=x+$\frac{1}{{e}^{x}}$．
（1）讨论函数f（x）的单调性，并求其最值；
（2）若对任意的x∈（0，+∞），有f（x）＞ax2-1恒成立，求实数a的取值范围．
5．如图，阴影部分（包括边界）为平面区域D，若点P（x，y）在区域D内，则z=x+2y的最小值是-1；x，y满足的约束条件是$\left\{\begin{array}{l}2x-y+2≥0\\ x≤0\\ y≥0.\end{array}\right.$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网