题目内容
已知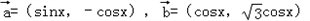 ,函数
,函数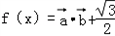 .
.
(1)求f(x)的最小正周期,并求其图象对称中心的坐标;
(2)当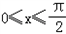 时,求函数f(x)的值域.
时,求函数f(x)的值域.
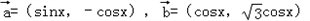 ,函数
,函数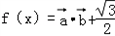 .
.(1)求f(x)的最小正周期,并求其图象对称中心的坐标;
(2)当
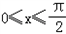 时,求函数f(x)的值域.
时,求函数f(x)的值域.解:(1)∵f(x)=sinxcosx﹣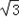 cos2x+
cos2x+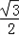 =
= sin2x﹣
sin2x﹣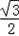 (cos2x+1)+
(cos2x+1)+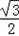
= sin2x﹣
sin2x﹣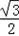 cos2x=sin(2x﹣
cos2x=sin(2x﹣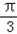 )
)
∴f(x)的最小正周期为π,令sin(2x﹣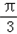 )=0,得
)=0,得
2x﹣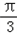 =kπ,
=kπ,
∴x=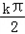 +
+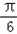 ,(k∈Z).
,(k∈Z).
故所求对称中心的坐标为(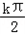 +
+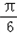 ,0),(k∈Z)
,0),(k∈Z)
(2)∵0≤x≤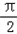 ,
,
∴﹣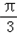 <2x﹣
<2x﹣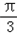 ≤
≤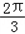
∴﹣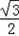 ≤sin(2x﹣
≤sin(2x﹣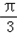 )≤1,
)≤1,
即f(x)的值域为[﹣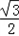 ,1]
,1]
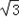 cos2x+
cos2x+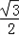 =
= sin2x﹣
sin2x﹣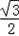 (cos2x+1)+
(cos2x+1)+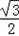
=
 sin2x﹣
sin2x﹣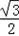 cos2x=sin(2x﹣
cos2x=sin(2x﹣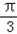 )
) ∴f(x)的最小正周期为π,令sin(2x﹣
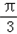 )=0,得
)=0,得2x﹣
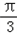 =kπ,
=kπ,∴x=
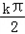 +
+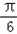 ,(k∈Z).
,(k∈Z).故所求对称中心的坐标为(
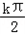 +
+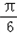 ,0),(k∈Z)
,0),(k∈Z)(2)∵0≤x≤
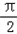 ,
,∴﹣
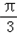 <2x﹣
<2x﹣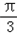 ≤
≤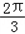
∴﹣
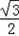 ≤sin(2x﹣
≤sin(2x﹣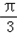 )≤1,
)≤1,即f(x)的值域为[﹣
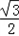 ,1]
,1]
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
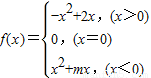 ,
, ;
; 的图象;
的图象; 在区间[-1,|
在区间[-1,| |-2]上单调递增,试确定
|-2]上单调递增,试确定 .
. 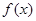 的最小正周期和当
的最小正周期和当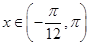 时的值域;
时的值域;
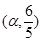 ,
,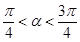 .求
.求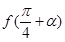 的值.
的值. .
. 的值;
的值; ,
, ,求
,求 的值.
的值. ,函数
,函数 .
. 的单调递减区间;
的单调递减区间; 在区间
在区间 上有极值,求
上有极值,求 的取值范围;
的取值范围;