题目内容
已知:
(1)求

(2)求满足条件
 的实数m,n.
的实数m,n.(3)若向量
 满足
满足 ,且
,且 求
求 .
.
【答案】分析:(1)由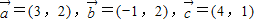 ,我们易求出
,我们易求出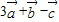 的坐标,代入向量模的公式,即可得到答案.
的坐标,代入向量模的公式,即可得到答案.
(2)由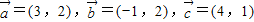 及
及 ,我们可构造一个关于m,n的方程组,解方程组,即可得到实数m,n的值.
,我们可构造一个关于m,n的方程组,解方程组,即可得到实数m,n的值.
(3)若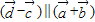 ,由向量的共线定理,我们易得
,由向量的共线定理,我们易得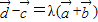 ,又由
,又由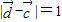 ,我们可以得到一个关于λ的方程,解方程求出λ的值,进而求以求出向量
,我们可以得到一个关于λ的方程,解方程求出λ的值,进而求以求出向量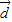 的坐标.
的坐标.
解答:解:(1) =(4,7)(3分)
=(4,7)(3分)
∴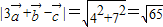 (5分)
(5分)
(2)由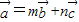 得
得
(3,2)=m(-1,2)+n(4,1)=(-m+4n,2m+n)(6分)
∴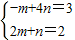 (8分)
(8分)
∴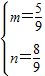 (10分)
(10分)
(3)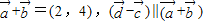
∴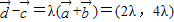 (λ∈R)(11分)
(λ∈R)(11分)
∴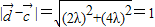 ∴
∴ (14分)
(14分)
∴ ,(15分)
,(15分)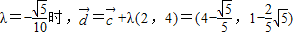 .(16分)
.(16分)
点评:判断两个向量的关系(平行或垂直)或是已知两个向量的关系求未知参数的值,要熟练掌握向量平行(共线)及垂直的坐标运算法则,即“两个向量若平行,交叉相乘差为0,两个向量若垂直,对应相乘和为0”.
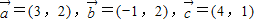 ,我们易求出
,我们易求出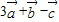 的坐标,代入向量模的公式,即可得到答案.
的坐标,代入向量模的公式,即可得到答案.(2)由
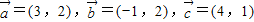 及
及 ,我们可构造一个关于m,n的方程组,解方程组,即可得到实数m,n的值.
,我们可构造一个关于m,n的方程组,解方程组,即可得到实数m,n的值.(3)若
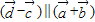 ,由向量的共线定理,我们易得
,由向量的共线定理,我们易得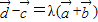 ,又由
,又由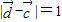 ,我们可以得到一个关于λ的方程,解方程求出λ的值,进而求以求出向量
,我们可以得到一个关于λ的方程,解方程求出λ的值,进而求以求出向量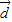 的坐标.
的坐标.解答:解:(1)
 =(4,7)(3分)
=(4,7)(3分)∴
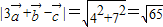 (5分)
(5分)(2)由
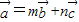 得
得(3,2)=m(-1,2)+n(4,1)=(-m+4n,2m+n)(6分)
∴
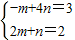 (8分)
(8分)∴
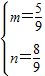 (10分)
(10分)(3)
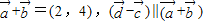
∴
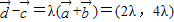 (λ∈R)(11分)
(λ∈R)(11分)∴
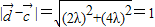 ∴
∴ (14分)
(14分)∴
 ,(15分)
,(15分)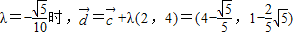 .(16分)
.(16分)点评:判断两个向量的关系(平行或垂直)或是已知两个向量的关系求未知参数的值,要熟练掌握向量平行(共线)及垂直的坐标运算法则,即“两个向量若平行,交叉相乘差为0,两个向量若垂直,对应相乘和为0”.

练习册系列答案
相关题目


 的单调区间
的单调区间


 的取值范围.
的取值范围.

 的单调区间
的单调区间