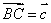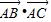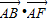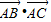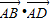题目内容
 如图,在边长为1的正方形ABCD中,E为BC的中点,若F为正方形内(含边界)任意一点,则
如图,在边长为1的正方形ABCD中,E为BC的中点,若F为正方形内(含边界)任意一点,则| AE |
| AF |
分析:先设出点A以及点F的坐标,求出其它各点的坐标,并利用点的坐标表示出
•
,把所求问题转化为在平面区域内求线性目标函数的最值问题求解即可.
| AE |
| AF |
解答: 解;可设点A(0,0),则B(1,0),C(1,1),D(0,1),E(1,
解;可设点A(0,0),则B(1,0),C(1,1),D(0,1),E(1,
),
设F(x,y),则
,对应的平面区域如图:
因为
=(1,
),
=(x,y).
所以
•
=x+
y.
借助于图象得当x+
y过点C(1,1)时取最大值,此时x+
y=
.
故答案为
.
 解;可设点A(0,0),则B(1,0),C(1,1),D(0,1),E(1,
解;可设点A(0,0),则B(1,0),C(1,1),D(0,1),E(1,| 1 |
| 2 |
设F(x,y),则
|
因为
| AE |
| 1 |
| 2 |
| AF |
所以
| AE |
| AF |
| 1 |
| 2 |
借助于图象得当x+
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
故答案为
| 3 |
| 2 |
点评:本题主要考查向量在几何中的应用以及数形结合思想的应用和转化思想的应用,是对基础知识和基本思想的考查,属于基础题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
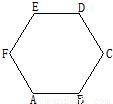
如图,在边长为1的正六边形ABCDEF中,下列向量的数量积中最大的是( )
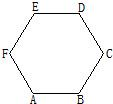

A、
| ||||
B、
| ||||
C、
| ||||
D、
|