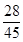题目内容
在10件产品中有2件次品,连续抽3次,每次抽1个,求:(1)不放回抽样时,抽到次品数X的分布列;
(2)放回抽样时,抽到次品Y的分布列(保留三位有效数字).
分析:首先确定X和Y的可取值,然后求出每种取值下的随机事件的概率,列出对应表格即为分布列.
解:(1)不放回抽样,抽到的次品数X=0,1,2,而P(X=0)=![]() ,P(X=1)=
,P(X=1)=![]() ,P(X=2)=
,P(X=2)=
![]() =
=![]() ,故X的分布列为:
,故X的分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
(2)放回抽样时,抽到的次品数Y=0,1,2,3,而P(Y=0)?=0.83=0.512,P(Y=1)=C![]() (0.8)2×0.2=0.384,P(Y=2)=C
(0.8)2×0.2=0.384,P(Y=2)=C![]() ·0.8×(0.2)2=0.096,P(Y=3)=0.23=0.008.
·0.8×(0.2)2=0.096,P(Y=3)=0.23=0.008.
故Y的分布列为:
Y | 0 | 1 | 2 | 3 |
P | 0.512 | 0.384 | 0.096 | 0.0088 |
绿色通道:从本例中可以看出超几何分布与二项分布的区别与联系:超几何分布是不放回抽样;二项分布是有放回抽样.

练习册系列答案
相关题目
已知在10件产品中有2件次品,现从中任意抽取2件产品,则至少抽出1件次品的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
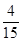 B.
B.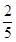 C.
C.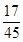 D.
D.