题目内容
已知函数f(x)= ,其中
,其中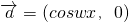 ,
,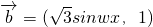 ,且w为正实数.
,且w为正实数.
(1)求f(x)的最小值;
(2)对任意m∈R,函数y=f(x),x∈[m,m+4π]的图象与直线2y+1=0有且仅有一个交点,试判断函数f(x+ )的奇偶性,并说明理由.
)的奇偶性,并说明理由.
解:(1)∵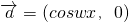 ,
, =(
=( siωx+cosωx,1),
siωx+cosωx,1),
函数 f(x)= =cosωx(
=cosωx( sinωx+cosωx)+0=
sinωx+cosωx)+0= sinωx•cosωx+cos2ωx
sinωx•cosωx+cos2ωx
= sin2ωx+
sin2ωx+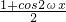 =sin(2ωx+
=sin(2ωx+ )+
)+ .
.
故函数 f(x)的最小值为-1+ =-
=- .
.
(2)由题意可得,函数的周期为4π,故 =4π,ω=
=4π,ω= .
.
∴f(x+ )=sin(
)=sin( x+
x+ +
+ )+
)+ =cos(
=cos( )+
)+ =cos(-
=cos(- )+
)+ ,x∈R,
,x∈R,
故函数f(x+ ) 为偶函数.
) 为偶函数.
分析:(1)利用两个向量的数量积公式,两角和的正弦公式化简函数f(x)=sin(2ωx+ )+
)+ ,由此求得它的最小值.
,由此求得它的最小值.
(2)由题意可得,函数的周期为4π,由此求得ω的值,化简函数f(x+ )的解析式cos(
)的解析式cos( )+
)+ ,可得函数为偶函数.
,可得函数为偶函数.
点评:本题主要考查两个向量的数量积公式,两角和的正弦公式,余弦函数的奇偶性,诱导公式的应用,属于中档题.
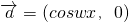 ,
, =(
=( siωx+cosωx,1),
siωx+cosωx,1),函数 f(x)=
 =cosωx(
=cosωx( sinωx+cosωx)+0=
sinωx+cosωx)+0= sinωx•cosωx+cos2ωx
sinωx•cosωx+cos2ωx=
 sin2ωx+
sin2ωx+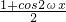 =sin(2ωx+
=sin(2ωx+ )+
)+ .
.故函数 f(x)的最小值为-1+
 =-
=- .
.(2)由题意可得,函数的周期为4π,故
 =4π,ω=
=4π,ω= .
.∴f(x+
 )=sin(
)=sin( x+
x+ +
+ )+
)+ =cos(
=cos( )+
)+ =cos(-
=cos(- )+
)+ ,x∈R,
,x∈R,故函数f(x+
 ) 为偶函数.
) 为偶函数.分析:(1)利用两个向量的数量积公式,两角和的正弦公式化简函数f(x)=sin(2ωx+
 )+
)+ ,由此求得它的最小值.
,由此求得它的最小值.(2)由题意可得,函数的周期为4π,由此求得ω的值,化简函数f(x+
 )的解析式cos(
)的解析式cos( )+
)+ ,可得函数为偶函数.
,可得函数为偶函数.点评:本题主要考查两个向量的数量积公式,两角和的正弦公式,余弦函数的奇偶性,诱导公式的应用,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|