��Ŀ����
����Ŀ�������꣬���ڻ�������Ⱦ������Խ��Խ���أ�ij������˾����һ��PM2.5���������������������ӭ����֪���ֿ��ֵĽ���Ϊ40Ԫ�����������в����������y������������۵���x��Ԫ��������ͼ��ʾ��һ�κ�����ϵ��ÿ���������ֿ��ֵ��ܿ�֧z����Ԫ�����������ۣ���������y����������ں�����ϵz=10y+42.5�� 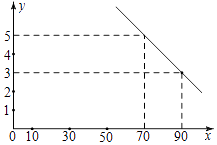
��I����y����x�ĺ�����ϵ��
��II��д���ù�˾�������ֿ��������W����Ԫ���������۵���x��Ԫ���ĺ�����ϵʽ
�������=�������ܽ������ۿ��ֵ��ܽ��۩����ܿ�֧���������۵���xΪ��ֵʱ�����������������Ƕ��٣�
��III������˾ϣ���ÿ���һ������ۻ���������57.5��Ԫ����ù�˾���ֿ��ֵ����۵���Ӧ����ʲô��Χ���ڴ�������Ҫʹ���ֵ��������������Ϊ���۵���Ӧ��Ϊ����Ԫ��
���𰸡��⣺��I�������⣬��y=kx+b��ͼ����㣨70��5������90��3���� ![]() ����k=��
����k=�� ![]() ��b=12��
��b=12��
�� ![]()
��II�� �����⣬��
w=y��x��40����z
=y��x��40������10y+42.5��
=���� ![]() x+12����x��40����10����
x+12����x��40����10���� ![]() x+12����42.5
x+12����42.5
=��0.1x2+17x��642.5=�� ![]() ��x��85��2+80��
��x��85��2+80��
�����۵���Ϊ85Ԫʱ�������������ֵΪ80��Ԫ
��III����W��57.5����0.1x2+17x��642.5��57.5��
������x2��170x+7000��0�����70��x��100��
��Ҫʹ�ÿ���һ������ۻ���������57.5��Ԫ������Ӧ��70Ԫ��100Ԫ֮�䣮
����Ϊ���۵���Խ�ͣ�������Խ������Ҫʹ����������һ���������57.5��Ԫ�����۵���Ӧ��Ϊ70Ԫ��
����������I����ͼ���֪y����x�ĺ�����ϵʽ��һ�κ�������y=kx+b���á����㷨���������ʽ����II�����������=�������ܽ��һ�����۲�Ʒ���ܽ���һ���ܿ�֧���г�������ϵʽ����III����W��57.5���Ӷ�ȷ�����۵���x�ķ�Χ�������κ���w���ʱ��x��ֵ��

 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д�