题目内容
函数y=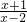
的单调区间是
- A.（-∞，-1），（-1，+∞）
- B.（-2，+∞），（-∞，-2）
- C.（-∞，2），（2，+∞）
- D.（-∞，2）∪（2，+∞）
C
分析：根据函数的解析式求出函数导函数的解析式，进而分析出导函数在定义域各区间上的符号，进而分析出函数的单调性
解答：∵y=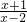
∴y′=
=
当x∈（-∞，2）或x∈（2，+∞）时，y′＜0恒成立
故函数y=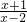的单调区间是（-∞，2），（2，+∞）
故选C
点评：本题考查的知识点是函数的单调性及单调区间，解答时易忽略函数的图象是不连续的，而错选D
分析：根据函数的解析式求出函数导函数的解析式，进而分析出导函数在定义域各区间上的符号，进而分析出函数的单调性
解答：∵y=
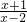
∴y′=
=当x∈（-∞，2）或x∈（2，+∞）时，y′＜0恒成立
故函数y=
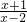的单调区间是（-∞，2），（2，+∞）故选C
点评：本题考查的知识点是函数的单调性及单调区间，解答时易忽略函数的图象是不连续的，而错选D
练习册系列答案
优加精卷系列答案
相关题目
在（-∞，-1）∪（-1，+∞）上是减函数；③函数y=
的单调区间是[-2，+∞）；④已知f（x）在R上是增函数，若a+b＞0，则有f（a）+f（b）＞f（-a）+f（-b）．其中正确命题的序号是________．
在（-∞，-1）∪（-1，+∞）上是减函数；③函数y=
的单调区间是[-2，+∞）；④已知f（x）在R上是增函数，若a+b＞0，则有f（a）+f（b）＞f（-a）+f（-b）．其中正确命题的序号是 ．
在（-∞，-1）∪（-1，+∞）上是减函数；③函数y=
的单调区间是[-2，+∞）；④已知f（x）在R上是增函数，若a+b＞0，则有f（a）+f（b）＞f（-a）+f（-b）．其中正确命题的序号是 ．
在（-∞，-1）∪（-1，+∞）上是减函数；③函数y=
的单调区间是[-2，+∞）；④已知f（x）在R上是增函数，若a+b＞0，则有f（a）+f（b）＞f（-a）+f（-b）．其中正确命题的序号是 ．