题目内容
已知函数 ,若|f(x)|≥ax,则实数a的取值范围为( )
,若|f(x)|≥ax,则实数a的取值范围为( )A.(-∞,-ln2]
B.(-∞,1]
C.(-ln2,1]
D.[-ln2,0]
【答案】分析:先画函数 的图象,根据图象可知,f(x)≥0,从而|f(x)|≥ax,即f(x)≥ax,根据图象可直接得出答案.
的图象,根据图象可知,f(x)≥0,从而|f(x)|≥ax,即f(x)≥ax,根据图象可直接得出答案.
解答: 解:画函数
解:画函数 的图象,如图所示.
的图象,如图所示.
∵f(x)≥0,∴|f(x)|≥ax?f(x)≥ax,
从图象上看,即要使得直线y=ax都在y=f(x)图象的下方,
故a≤0,且y= 在x=0处的切线的斜率k≤a.
在x=0处的切线的斜率k≤a.
又y'=[ ]'=
]'= ,
,
∴y= 在x=0处的切线的斜率k=-ln2
在x=0处的切线的斜率k=-ln2
∴-ln2≤a≤0.
故选D.
点评:本题主要考查指数、对数函数的图象,考查数形结合思想,考查函数与方程的综合运用,华罗庚曾说过:“数缺形时少直观,形缺数时难入微.数形结合百般好,隔离分家万事非.”数形结合是数学解题中常用的思想方法.属中档题.
 的图象,根据图象可知,f(x)≥0,从而|f(x)|≥ax,即f(x)≥ax,根据图象可直接得出答案.
的图象,根据图象可知,f(x)≥0,从而|f(x)|≥ax,即f(x)≥ax,根据图象可直接得出答案.解答:
 解:画函数
解:画函数 的图象,如图所示.
的图象,如图所示.∵f(x)≥0,∴|f(x)|≥ax?f(x)≥ax,
从图象上看,即要使得直线y=ax都在y=f(x)图象的下方,
故a≤0,且y=
 在x=0处的切线的斜率k≤a.
在x=0处的切线的斜率k≤a.又y'=[
 ]'=
]'= ,
,∴y=
 在x=0处的切线的斜率k=-ln2
在x=0处的切线的斜率k=-ln2∴-ln2≤a≤0.
故选D.
点评:本题主要考查指数、对数函数的图象,考查数形结合思想,考查函数与方程的综合运用,华罗庚曾说过:“数缺形时少直观,形缺数时难入微.数形结合百般好,隔离分家万事非.”数形结合是数学解题中常用的思想方法.属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
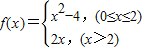 ,若f(x)=12,则x= .
,若f(x)=12,则x= .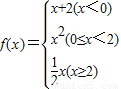 ,若f(x)=2,则x的值为( )
,若f(x)=2,则x的值为( )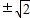
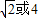
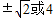
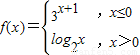 ,若f(x)≥1,则x的取值范围为 .
,若f(x)≥1,则x的取值范围为 .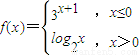 ,若f(x)≥1,则x的取值范围为 .
,若f(x)≥1,则x的取值范围为 .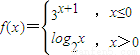 ,若f(x)≥1,则x的取值范围为 .
,若f(x)≥1,则x的取值范围为 .