题目内容
设函数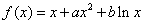 ,曲线
,曲线 过P(1,0),且在P点处的切斜线率为2.
过P(1,0),且在P点处的切斜线率为2.
(I)求a,b的值;(II)证明: .
.
(I)
由已知条件得 ,解得
,解得
(II) ,由(I)知
,由(I)知
设 则
则




练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
题目内容
设函数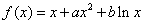 ,曲线
,曲线 过P(1,0),且在P点处的切斜线率为2.
过P(1,0),且在P点处的切斜线率为2.
(I)求a,b的值;(II)证明: .
.
(I)
由已知条件得 ,解得
,解得
(II) ,由(I)知
,由(I)知
设 则
则




 优学名师名题系列答案
优学名师名题系列答案