题目内容
14.在△ABC中,若A,B,C所对边的长分别为a,b,c,若a=2,B=$\frac{π}{6}$,c=2$\sqrt{3}$,则b=( )| A. | 4 | B. | 2 | C. | 3 | D. | 1 |
分析 由已知及余弦定理b2=a2+c2-2accosB即可得解.
解答 解:∵a=2,B=$\frac{π}{6}$,c=2$\sqrt{3}$,
∴由余弦定理b2=a2+c2-2accosB=4+12-2×2×2$\sqrt{3}$cos$\frac{π}{6}$=4,
解之得b=2.
故选:B.
点评 本题主要考查了余弦定理的应用,属于基础题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
4.已知f(x)、g(x)均为[-1,3]上连续不断的曲线,根据下表能判断方程f(x)=g(x)有实数解的区间是( )
| x | -1 | 0 | 1 | 2 | 3 |
| f(x) | -0.677 | 3.011 | 5.432 | 5.980 | 7.651 |
| g(x) | -0.530 | 3.451 | 4.890 | 5.241 | 6.892 |
| A. | (-1,0) | B. | (1,2) | C. | (0,1) | D. | (2,3) |
2.函数y=f(x)的图象在点x=5处的切线方程是y=-x+8,则f(5)+f′(5)=( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
19.如图,直线y=kx分抛物线y=x-x2与x轴所围图形为上下两部分面积比为1:7,则k的值为( )
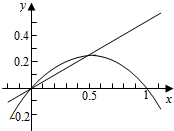

| A. | 1 | B. | $\sqrt{2}$-1 | C. | 0.5 | D. | 0.4 |
6.已知条件p:|5x-2|>3,q:$\frac{1}{{x}^{2}+4x-5}>0$,则“¬p”是“¬q”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |