题目内容
如图,直三棱柱ABC—A1B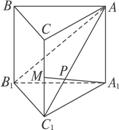
证明:如图,连结AC1交A

∵∠BCA=90°,且BC⊥CC1,
∴BC⊥平面AA
又BC∥B
∴AC1是AB1在平面AA
设∠AC![]() ,tanβ=
,tanβ=![]()
![]() .
.
∴α+β=90°,即AC1⊥A
∴AB1⊥A

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
题目内容
如图,直三棱柱ABC—A1B
证明:如图,连结AC1交A

∵∠BCA=90°,且BC⊥CC1,
∴BC⊥平面AA
又BC∥B
∴AC1是AB1在平面AA
设∠AC![]() ,tanβ=
,tanβ=![]()
![]() .
.
∴α+β=90°,即AC1⊥A
∴AB1⊥A

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案