题目内容
已知函数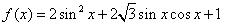 ,x∈R。求:
,x∈R。求:
(I) 函数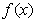 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(II)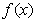 在
在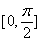 上的最值;
上的最值;
(Ⅲ)该函数的图像经过怎样的平移和伸缩变换可以得到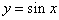 (x∈R)的图像?
(x∈R)的图像?
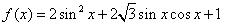 ,x∈R。求:
,x∈R。求:(I) 函数
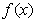 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;(II)
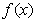 在
在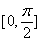 上的最值;
上的最值; (Ⅲ)该函数的图像经过怎样的平移和伸缩变换可以得到
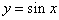 (x∈R)的图像?
(x∈R)的图像? 解:(Ⅰ) ,
,
∴ ,
,
由 得
得
 ,
,
故函数的单调递增区间为 。
。
(Ⅱ)当 时,
时,
∴ ,
,
∴ ,
,
∴ ,
, 。
。
(Ⅲ)向下平移2个单位,横坐标不变,纵坐标缩短为原来的 ,纵坐标不变,横坐标扩大为原来的
,纵坐标不变,横坐标扩大为原来的
2倍,向左平移 个单位。
个单位。
 ,
,∴
 ,
,由
 得
得 ,
,故函数的单调递增区间为
 。
。(Ⅱ)当
 时,
时,
∴
 ,
,∴
 ,
,∴
 ,
, 。
。(Ⅲ)向下平移2个单位,横坐标不变,纵坐标缩短为原来的
 ,纵坐标不变,横坐标扩大为原来的
,纵坐标不变,横坐标扩大为原来的2倍,向左平移
 个单位。
个单位。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
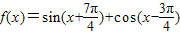 ,x∈R,求f(x)的最小正周期和在[0,
,x∈R,求f(x)的最小正周期和在[0,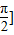 上的最小值和最大值.
上的最小值和最大值.