题目内容
已知椭圆C: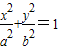 (a>b>0)的两个焦点和短轴的两个端点都在圆x2+y2=1上.
(a>b>0)的两个焦点和短轴的两个端点都在圆x2+y2=1上.(I)求椭圆C的方程;
(Ⅱ)若斜率为k的直线过点M(2,0),且与椭圆C相交于A,B两点.试探讨k为何值时,三角形OAB为直角三角形.
【答案】分析:(Ⅰ)由题意可知b和c,利用隐含条件求出a,则椭圆方程可求;
(Ⅱ)设出直线AB的方程,联立直线方程和椭圆方程,由判别式大于0求出k的范围,利用根与系数关系得到A与B的横坐标的和与积,讨论O与A(或B)为直角顶点两种情况,O为直角顶点时,直接由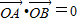 列式求解k的值,若A(或B)为直角顶点时,由斜率之积等于-1求出OA的斜率,由两直线联立解出A点(或B)点坐标,代入椭圆方程求得k的值.
列式求解k的值,若A(或B)为直角顶点时,由斜率之积等于-1求出OA的斜率,由两直线联立解出A点(或B)点坐标,代入椭圆方程求得k的值.
解答:解:(Ⅰ)因为焦点与短轴的端点都在圆x2+y2=1上,
∴c=1,b=1,
∴a2=b2+c2=1+1=2.
则椭圆方程为: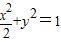 ;
;
(Ⅱ)由已知直线AB的斜率存在,设直线AB的方程为y=k(x-2).
联立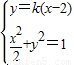 ,得(1+k2)x2-8k2x+8k2-2=0.
,得(1+k2)x2-8k2x+8k2-2=0.
由△=64k4-4(1+k2)(8k2-2)>0,得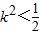 .
.
所以k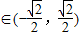 .
.
设A(x1,y1),B(x2,y2).
则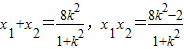 .
.
若O为直角顶点,则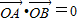 ,即x1x2+y1y2=0.
,即x1x2+y1y2=0.
y1y2=k(x1-2)k(x2-2).
所以上式可整理得: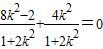 .
.
解得k=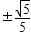 .满足k
.满足k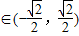 .
.
若A或B为直角顶点,不妨设A为直角顶点,
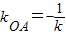 ,则A满足
,则A满足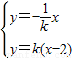 ,解得
,解得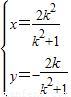
代入椭圆方程得k4+2k2-1=0.
解得k=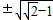 .满足k
.满足k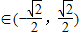 .
.
综上,k=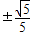 或k=
或k=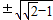 时三角形OAB为直角三角形.
时三角形OAB为直角三角形.
点评:本题考查了椭圆的标准方程,考查了直线和圆锥曲线的关系,考查了分类讨论的数学思想方法哈数学转化思想方法,训练了平面向量在解题中的应用,考查了学生的计算能力,是难题.
(Ⅱ)设出直线AB的方程,联立直线方程和椭圆方程,由判别式大于0求出k的范围,利用根与系数关系得到A与B的横坐标的和与积,讨论O与A(或B)为直角顶点两种情况,O为直角顶点时,直接由
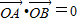 列式求解k的值,若A(或B)为直角顶点时,由斜率之积等于-1求出OA的斜率,由两直线联立解出A点(或B)点坐标,代入椭圆方程求得k的值.
列式求解k的值,若A(或B)为直角顶点时,由斜率之积等于-1求出OA的斜率,由两直线联立解出A点(或B)点坐标,代入椭圆方程求得k的值.解答:解:(Ⅰ)因为焦点与短轴的端点都在圆x2+y2=1上,
∴c=1,b=1,
∴a2=b2+c2=1+1=2.
则椭圆方程为:
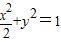 ;
;(Ⅱ)由已知直线AB的斜率存在,设直线AB的方程为y=k(x-2).
联立
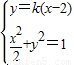 ,得(1+k2)x2-8k2x+8k2-2=0.
,得(1+k2)x2-8k2x+8k2-2=0.由△=64k4-4(1+k2)(8k2-2)>0,得
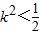 .
.所以k
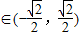 .
.设A(x1,y1),B(x2,y2).
则
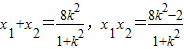 .
.若O为直角顶点,则
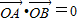 ,即x1x2+y1y2=0.
,即x1x2+y1y2=0.y1y2=k(x1-2)k(x2-2).
所以上式可整理得:
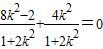 .
.解得k=
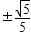 .满足k
.满足k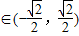 .
.若A或B为直角顶点,不妨设A为直角顶点,
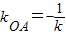 ,则A满足
,则A满足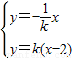 ,解得
,解得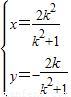
代入椭圆方程得k4+2k2-1=0.
解得k=
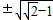 .满足k
.满足k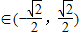 .
.综上,k=
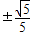 或k=
或k=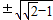 时三角形OAB为直角三角形.
时三角形OAB为直角三角形.点评:本题考查了椭圆的标准方程,考查了直线和圆锥曲线的关系,考查了分类讨论的数学思想方法哈数学转化思想方法,训练了平面向量在解题中的应用,考查了学生的计算能力,是难题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
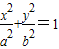 (a>b>0)的左、右焦点分别为F1(-1,0)、F2(1,0),离心率为
(a>b>0)的左、右焦点分别为F1(-1,0)、F2(1,0),离心率为 .
. (O为坐标原点),求△AOB的面积;
(O为坐标原点),求△AOB的面积;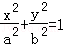 (a>b>0)的两个焦点分别为F1(﹣1,0),F2(1,0),且椭圆C经过点
(a>b>0)的两个焦点分别为F1(﹣1,0),F2(1,0),且椭圆C经过点 .
. ,求点Q的轨迹方程.
,求点Q的轨迹方程. (a>b>0)的一个顶点为A(2,0),离心率为
(a>b>0)的一个顶点为A(2,0),离心率为 ,直线y=k(x-1)与椭圆C交于不同的两点M、N.
,直线y=k(x-1)与椭圆C交于不同的两点M、N. 时,求k的值.
时,求k的值. +
+ =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+ 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同两点A,B且线段AB的垂直平分线过定点C(
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同两点A,B且线段AB的垂直平分线过定点C( ,0)求实数k的取值范围。
,0)求实数k的取值范围。 (a>b>0)的离心率为
(a>b>0)的离心率为 ,过右焦点F且斜率为k(k>0)的直线与椭圆C相交于A、B两点,若
,过右焦点F且斜率为k(k>0)的直线与椭圆C相交于A、B两点,若 。则
。则 ( )
( )  (D)
(D)