题目内容
设f(x)是定义在R上的偶函数,对任意x∈R,都有f(x-2)=f(x+2),且当x∈[-2,0]时,f(x)=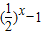 .若函数g(x)=f(x)-loga(x+2)(a>1)在区间(-2,6]恰有3个不同的零点,则a的取值范围是 .
.若函数g(x)=f(x)-loga(x+2)(a>1)在区间(-2,6]恰有3个不同的零点,则a的取值范围是 .
【答案】分析:由题意中f(x-2)=f(2+x),可得函数f(x)是一个周期函数,且周期为4,又由函数为偶函数,则可得f(x)在区间(-2,6]上的图象,结合方程的解与函数的零点之间的关系,可将方程f(x)-logax+2=0恰有3个不同的实数解,转化为两个函数图象恰有3个不同的交点,数形结合即可得到实数a的取值范围.
解答: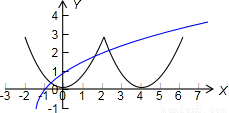 解:∵对于任意的x∈R,都有f(x-2)=f(2+x),
解:∵对于任意的x∈R,都有f(x-2)=f(2+x),
∴函数f(x)是一个周期函数,且T=4
又∵当x∈[-2,0]时,f(x)=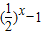 ,且函数f(x)是定义在R上的偶函数,
,且函数f(x)是定义在R上的偶函数,
故函数f(x)在区间(-2,6]上的图象如下图所示:
若在区间(-2,6]内关于x的方程f(x)-logax+2=0恰有3个不同的实数解
则loga4<3,loga8>3,
解得: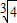 <a<2,
<a<2,
即a的取值范围是(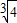 ,2);
,2);
故答案为(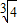 ,2).
,2).
点评:本题考查根的存在性及根的个数判断,关键是根据方程的解与函数的零点之间的关系,将方程根的问题转化为函数零点问题.
解答:
 解:∵对于任意的x∈R,都有f(x-2)=f(2+x),
解:∵对于任意的x∈R,都有f(x-2)=f(2+x),∴函数f(x)是一个周期函数,且T=4
又∵当x∈[-2,0]时,f(x)=
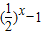 ,且函数f(x)是定义在R上的偶函数,
,且函数f(x)是定义在R上的偶函数,故函数f(x)在区间(-2,6]上的图象如下图所示:
若在区间(-2,6]内关于x的方程f(x)-logax+2=0恰有3个不同的实数解
则loga4<3,loga8>3,
解得:
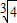 <a<2,
<a<2,即a的取值范围是(
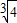 ,2);
,2);故答案为(
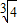 ,2).
,2).点评:本题考查根的存在性及根的个数判断,关键是根据方程的解与函数的零点之间的关系,将方程根的问题转化为函数零点问题.

练习册系列答案
相关题目
设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x).当x∈[0,2]时,f(x)=2x-x2+a(a是常数).则x∈[2,4]时的解析式为( )
| A、f(x)=-x2+6x-8 | B、f(x)=x2-10x+24 | C、f(x)=x2-6x+8 | D、f(x)=x2-6x+8+a |