题目内容
已知矩阵M=
|
分析:先根据特征值的定义列出特征多项式,令f(λ)=0解方程可得特征值,再由特征值列出方程组即可解得相应的特征向量.
解答:解:矩阵M的特征多项式为f(λ)=
=λ2-3λ+2,(2分)
令f(λ)=0,解得λ1=1,λ2=2,(4分)
将λ1=1代入二元一次方程组
解得x=0,(6分)
所以矩阵M属于特征值1的一个特征向量为
;(8分)
同理,矩阵M属于特征值2的一个特征向量为
(10分)
|
令f(λ)=0,解得λ1=1,λ2=2,(4分)
将λ1=1代入二元一次方程组
|
所以矩阵M属于特征值1的一个特征向量为
|
同理,矩阵M属于特征值2的一个特征向量为
|
点评:本题主要考查来了矩阵特征值与特征向量的计算等基础知识,属于基础题.

练习册系列答案
相关题目
 ,向量
,向量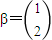 ,求向量α,使得A2α=β
,求向量α,使得A2α=β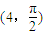 ,若直线l过点P,且倾斜角为
,若直线l过点P,且倾斜角为 ,圆C以M为圆心、4为半径.
,圆C以M为圆心、4为半径.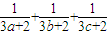 的最小值.
的最小值.