题目内容
设F1,F2为椭圆 的两个焦点,P在椭圆上,当△F1PF2面积为1时,则
的两个焦点,P在椭圆上,当△F1PF2面积为1时,则 的值是( )
的值是( )A.0
B.1
C.2
D.I
【答案】分析:设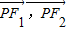 的夹角为2θ,根据焦点三角形面积公式S=b2tanθ,可求2θ,再利用数量积公式即可;
的夹角为2θ,根据焦点三角形面积公式S=b2tanθ,可求2θ,再利用数量积公式即可;
解答:解:设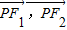 的夹角为2θ
的夹角为2θ
因为S=b2tanθ=1,其中b=1所以tanθ=1,θ=45°
∴∠F1PF2=90°
所以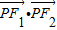 =0
=0
故选A
点评:本题以椭圆为载体,考查焦点三角形的面积,关键是利用椭圆的定义及面积公式S=b2tanθ.
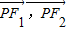 的夹角为2θ,根据焦点三角形面积公式S=b2tanθ,可求2θ,再利用数量积公式即可;
的夹角为2θ,根据焦点三角形面积公式S=b2tanθ,可求2θ,再利用数量积公式即可;解答:解:设
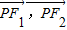 的夹角为2θ
的夹角为2θ因为S=b2tanθ=1,其中b=1所以tanθ=1,θ=45°
∴∠F1PF2=90°
所以
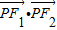 =0
=0故选A
点评:本题以椭圆为载体,考查焦点三角形的面积,关键是利用椭圆的定义及面积公式S=b2tanθ.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
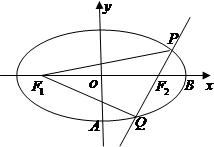 已知椭圆
已知椭圆