题目内容
(1)解不等式:-2x2-x+6≥0
(2)已知不等式x2-2x+k2-1>0对一切实数x恒成立,求实数k的取值范围.
(2)已知不等式x2-2x+k2-1>0对一切实数x恒成立,求实数k的取值范围.
(1)-2x2-x+6≥0
因式分解得:-(2x-3)(x+2)≥0,
即:(2x-3)(x+2)≤0,
解得:-2≤x≤
,
所以原不等式的解集是:[-2,
]
(2)∵不等式x2-2x+k2-1>0对一切实数x恒成立,
根据y=x2-2x+k2-1的图象
△<0,即4-4(k2-1)<0
解为k>
或k<-
,
∴k的取值范围是k>
或k<-
.
因式分解得:-(2x-3)(x+2)≥0,
即:(2x-3)(x+2)≤0,
解得:-2≤x≤
| 3 |
| 2 |
所以原不等式的解集是:[-2,
| 3 |
| 2 |
(2)∵不等式x2-2x+k2-1>0对一切实数x恒成立,
根据y=x2-2x+k2-1的图象
△<0,即4-4(k2-1)<0
解为k>
| 2 |
| 2 |
∴k的取值范围是k>
| 2 |
| 2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
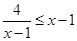
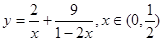 的最小值
的最小值
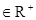 且
且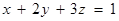 ,求
,求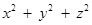 的最小值.
的最小值.