题目内容
(理)(1)已知集合P={x|
≤x≤2},函数f(x)=log2(ax2-2x+2)的定义域为Q,若P⊆Q,求实数a的取值范围;
(2)已知集合P={x|
≤x≤2},函数f(x)=log2(ax2-2x+2)的定义域为Q,若P∩Q≠∅,求实数a的取值范围.
| 1 |
| 2 |
(2)已知集合P={x|
| 1 |
| 2 |
分析:(1)P⊆Q,则说明不等式ax2-2x+2>0在x∈[
,2]上恒成立,分离参数后转化为函数最值问题即可解决;
(2)P∩Q≠∅,则说明在[
,2]上至少存在一个x值,使不等式ax2-2x+2>0成立,进而转化为函数最值问题解决;
| 1 |
| 2 |
(2)P∩Q≠∅,则说明在[
| 1 |
| 2 |
解答:解:(1)由已知Q={x|ax2-2x+2>0},
若P⊆Q,则说明不等式ax2-2x+2>0在x∈[
,2]上恒成立,
即不等式a>
-
在x∈[
,2]上恒成立,
令u=
-
,则只需a>umax即可.
又u=
-
=-2(
-
)2+
.
当x∈[
,2]时,
∈[
,2],从而u∈[-4,
],umax=
,
∴a>
.所以实数a的取值范围是a>
.
(2)若P∩Q≠∅,
则说明在[
,2]上至少存在一个x值,使不等式ax2-2x+2>0成立,
即在[
,2]上至少存在一个x值,使a>
-
成立,即只需a>umin即可.
由(1)知,umin=-4,∴a>-4.
若P⊆Q,则说明不等式ax2-2x+2>0在x∈[
| 1 |
| 2 |
即不等式a>
| 2 |
| x |
| 2 |
| x2 |
| 1 |
| 2 |
令u=
| 2 |
| x |
| 2 |
| x2 |
又u=
| 2 |
| x |
| 2 |
| x2 |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
当x∈[
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴a>
| 1 |
| 2 |
| 1 |
| 2 |
(2)若P∩Q≠∅,
则说明在[
| 1 |
| 2 |
即在[
| 1 |
| 2 |
| 2 |
| x |
| 2 |
| x2 |
由(1)知,umin=-4,∴a>-4.
点评:本题考查对数函数定义域的求解、集合运算及不等式恒成立问题,解决关键是恰当转化为函数最值.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 ,函数
,函数 的定义域为Q,若P⊆Q,求实数a的取值范围;
的定义域为Q,若P⊆Q,求实数a的取值范围;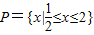 ,函数
,函数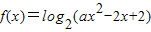 的定义域为Q,若P⊆Q,求实数a的取值范围;
的定义域为Q,若P⊆Q,求实数a的取值范围; ,函数
,函数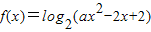 的定义域为Q,若P∩Q≠∅,求实数a的取值范围.
的定义域为Q,若P∩Q≠∅,求实数a的取值范围.