题目内容
设集合S={
}，在S上定义运算为：
=Ak,其中k为i+j被4除的余数，i、j=0,1,2,3.满足关系式
的x(x∈S)的个数为（ ）
| A．4 | B．3 | C．2 | D．1 |
C
解析试题分析：由定义
能满足关系式，同理x=A3满足关系式,故选C.
考点：集合的新定义
点评：解决的关键是对于集合的定义的准确理解，属于基础题。
练习册系列答案
相关题目
设集合
，
，
，且
，则
| A．1 | B．2 | C．3 | D．9 |
已知全集
,则
=（ ）
A． | B． |
C． | D． |
若函数
的值域为集合
，则下列元素中不属于的是 （ ）
| A．2 | B． | C． | D．1 |
设全集
，集合
，
，则图中的阴影部分表示的集合为（ ）
A． | B． | C． | D． |
已知集合
，集合
，则
( ).
| A．(0，2) | B．[0，2] | C．{0，2} | D．{0，1，2} |
已知全集U=R,集合A=
，集合B=
，则
为（ ）。
A． | B．R | C． | D． |
已知集合
，
是函数
的定义域，则
A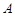． = | B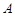． | C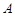． | D． Æ |