题目内容
已知直线y=k(x+2)(k>0)与抛物线C:y2=8x相交于A、B两点,F为C的焦点,若|FA|=2|FB|,则k等于( )
(A) 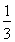 (B)
(B) 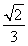 (C)
(C) 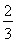 (D)
(D) 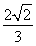
【答案】
D
【解析】将y=k(x+2)代入y2=8x,得
k2x2+(4k2-8)x+4k2=0.
设交点的横坐标分别为xA,xB,
则xA+xB= -4,①
-4,①
xA·xB=4.
又|FA|=xA+2,|FB|=xB+2,
|FA|=2|FB|,
∴2xB+4=xA+2.
∴xA=2xB+2.②
∴将②代入①得xB= -2,
-2,
xA= -4+2=
-4+2= -2.
-2.
故xA·xB= =4.
=4.
解之得k2= .
.
而k>0,∴k= ,满足Δ>0.故选D.
,满足Δ>0.故选D.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 :y=k(x+2
:y=k(x+2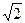 )与圆O:x2+y2=4相交于不重合的
)与圆O:x2+y2=4相交于不重合的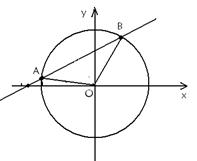
 :y=k(x+2
:y=k(x+2 )与圆O:x2+y2=4相交于不重合的
)与圆O:x2+y2=4相交于不重合的