题目内容
 如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2.
如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2.(I)求证:AF∥平面BDE;
(Ⅱ)求二面角B-DE-C的余弦值.
分析:(I)取BD的中点P,连接EP,FP,则PF
DC,由EA
DC,知四边形AFPE是平行四边形,由此能够证明AF∥面BDE.
(Ⅱ)以CA,CD所在直线分别作为x轴,z轴,以过C点和AB平行的直线作为y轴,建立空间直角坐标系,由DC=AC=2AE=2,得A(2,0,0),B(2,2,0),E(2,0,1),D(0,0,2),则
=(0,2,0),
=(0,-2,1),
=(-2,-2,2),由面ACDE⊥面ABC,面ACDE∩面ABC=AC,AB⊥AC,知
=(0,2,0)是平面CDE的一个法向量,由面BDE的一个法向量
=(1,1,2),能求出二面角B-DE-C的余弦值.
| ||
. |
| 1 |
| 2 |
| ||
. |
| 1 |
| 2 |
(Ⅱ)以CA,CD所在直线分别作为x轴,z轴,以过C点和AB平行的直线作为y轴,建立空间直角坐标系,由DC=AC=2AE=2,得A(2,0,0),B(2,2,0),E(2,0,1),D(0,0,2),则
| AB |
| BE |
| BD |
| AB |
| n |
解答: 解:(I)取BD的中点P,连接EP,FP,则PF
解:(I)取BD的中点P,连接EP,FP,则PF
DC,∵EA
DC,∴EA
PF,
∴四边形AFPE是平行四边形,∴AF∥EP,
又∵EP?面BDE,AF?平面BDE,
∴AF∥面BDE.
(Ⅱ)以CA,CD所在直线分别作为x轴,z轴,以过C点和AB平行的直线作为y轴,建立如图所示的空间直角坐标系,
由DC=AC=2AE=2,得A(2,0,0),B(2,2,0),E(2,0,1),D(0,0,2),
则
=(0,2,0),
=(0,-2,1),
=(-2,-2,2)
∵面ACDE⊥面ABC,面ACDE∩面ABC=AC,
AB⊥AC,∴AB⊥面ACDE,
∴
=(0,2,0)是平面CDE的一个法向量,
设面BDE的一个法向量
=(x,y,z),则
⊥
,
⊥
,
∴
,即
,
整理,得
,
令y=1,则z=2,x=1,∴
=(1,1,2)是平面CDE的一个法向量,
故cos<
,
>=
=
=
,
由图形知二面角B-DE-C的平面角θ∈(0,
),
所以二面角B-DE-C的余弦值为
.
 解:(I)取BD的中点P,连接EP,FP,则PF
解:(I)取BD的中点P,连接EP,FP,则PF
| ||
. |
| 1 |
| 2 |
| ||
. |
| 1 |
| 2 |
| ||
. |
∴四边形AFPE是平行四边形,∴AF∥EP,
又∵EP?面BDE,AF?平面BDE,
∴AF∥面BDE.
(Ⅱ)以CA,CD所在直线分别作为x轴,z轴,以过C点和AB平行的直线作为y轴,建立如图所示的空间直角坐标系,
由DC=AC=2AE=2,得A(2,0,0),B(2,2,0),E(2,0,1),D(0,0,2),
则
| AB |
| BE |
| BD |
∵面ACDE⊥面ABC,面ACDE∩面ABC=AC,
AB⊥AC,∴AB⊥面ACDE,
∴
| AB |
设面BDE的一个法向量
| n |
| n |
| BE |
| n |
| BD |
∴
|
|
整理,得
|
令y=1,则z=2,x=1,∴
| n |
故cos<
| AB |
| n |
| ||||
|
|
| 1×2 | ||
2×
|
| ||
| 6 |
由图形知二面角B-DE-C的平面角θ∈(0,
| π |
| 2 |
所以二面角B-DE-C的余弦值为
| ||
| 6 |
点评:本题考查直线与平面平行的证明,二查二面角的余弦值的求法,解题时要认真审题上,合理地化空间问题为平面问题,注意向量法的合理运用.

练习册系列答案
相关题目
 如图所示,直角梯形ABCD绕边AD所在直线旋转一周形成的面所围成的旋转体是( )
如图所示,直角梯形ABCD绕边AD所在直线旋转一周形成的面所围成的旋转体是( ) (2013•永州一模)如图所示,直角梯形ABCD中,∠A=∠D=90°,AD=2,AB=3,CD=4,P在线段AB上,BP=1,O在CD上,且OP∥AD,将图甲沿OP折叠使得平面OCBP⊥底面ADOP,得到一个多面体(如图乙),M、N分别是AC、OP的中点.
(2013•永州一模)如图所示,直角梯形ABCD中,∠A=∠D=90°,AD=2,AB=3,CD=4,P在线段AB上,BP=1,O在CD上,且OP∥AD,将图甲沿OP折叠使得平面OCBP⊥底面ADOP,得到一个多面体(如图乙),M、N分别是AC、OP的中点.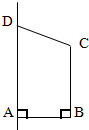
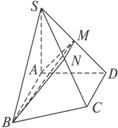
 如图所示,直角梯形ABCD绕边AD所在直线旋转一周形成的面所围成的旋转体是( )
如图所示,直角梯形ABCD绕边AD所在直线旋转一周形成的面所围成的旋转体是( )