题目内容
11．角θ的终边与单位圆的交点的横坐标为$-\frac{1}{2}$，则tanθ的值为（ ）| A． | $-\sqrt{3}$ | B． | ±1 | C． | $±\sqrt{3}$ | D． | $±\frac{{\sqrt{3}}}{3}$ |
分析 由条件利用任意角的三角函数的定义，求得tanθ的值．
解答 解：角θ的终边与单位圆的交点的横坐标为x=$-\frac{1}{2}$，则它的纵坐标为y=±$\frac{\sqrt{3}}{2}$，
故tanθ=$\frac{y}{x}$=±$\sqrt{3}$，
故选：C．
点评 本题主要考查任意角的三角函数的定义，属于基础题．
练习册系列答案
相关题目
16．已知直线l：x-my+$\sqrt{3}$m=0上存在点M满足与两点A（-1，0），B（1，0）连线的斜率kMA与kMB之积为3，则实数m的取值范围是（ ）
| A． | $[{-\sqrt{6}，\sqrt{6}}]$ | B． | $（{-∞，-\frac{{\sqrt{6}}}{6}}）$∪$（{\frac{{\sqrt{6}}}{6}，+∞}）$ | C． | $（{-∞，-\frac{{\sqrt{6}}}{6}}]$∪$[{\frac{{\sqrt{6}}}{6}，+∞}）$ | D． | 以上都不对 |
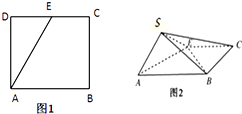如图，点E为正方形ABCD边CD上异于点C，D的动点，将△ADE沿AE翻折成△SAE，使得平面SAE⊥平面ABCE，则下列三个说法中正确的个数是（ ）
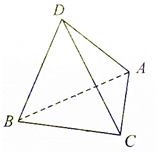如图，A、B、C、D为空间四点，△ABC中，AB=AC=BC=2，等边三角形ADB以AB为轴运动，当平面ADB⊥平面ABC时，则CD=$\sqrt{6}$．