题目内容
定义函数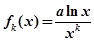 为
为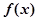 的
的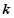 阶函数.
阶函数.
(1)求一阶函数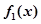 的单调区间;
的单调区间;
(2)讨论方程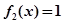 的解的个数;
的解的个数;
(3)求证: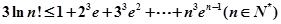 .
.
【答案】
(1)当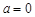 时,
时,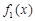 无单调区间;
无单调区间;
当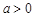 时,
时,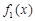 的单增区间为
的单增区间为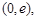 单减区间为
单减区间为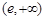 ;
;
当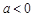 时,
时,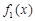 的单增区间为
的单增区间为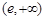 ,单减区间为
,单减区间为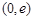 ;
;
(2)当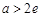 时,方程有两个不同解.当
时,方程有两个不同解.当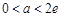 时,方程有0个解.当
时,方程有0个解.当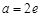 或
或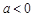 时,方程有唯一;
时,方程有唯一;
(3)详见解析.
【解析】
试题分析:(1)求导,对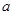 分情况讨论;
分情况讨论;
(2)研究方程的解的个数,实质就是研究函数的图象.通过求导,弄清函数的单调区间及函数值的范围,结合图象即可知道方程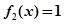 的解的个数.
的解的个数.
(3)待证不等式 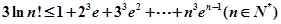
可变为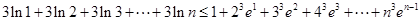 ,左右对照,考虑证:
,左右对照,考虑证:
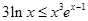
再联系到本题所给函数,可令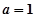 ,且研究
,且研究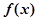 的3阶函数,即
的3阶函数,即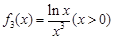 .
.
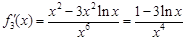 .由
.由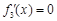 得
得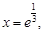
则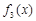 在
在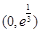 单调递增,在
单调递增,在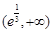 单调递减.
单调递减.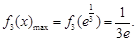
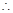
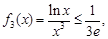 即
即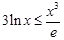 .又
.又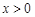 时,
时,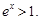
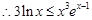
再令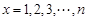 即得证.
即得证.
令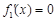 ,当
,当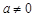 时,
时,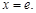
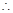 当
当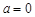 时,
时,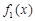 无单调区间;
无单调区间;
当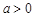 时,
时,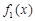 的单增区间为
的单增区间为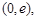 单减区间为
单减区间为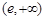 .
.
当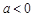 时,
时,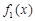 的单增区间为
的单增区间为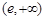 ,单减区间为
,单减区间为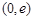 .
. 4分.
4分.
(2)由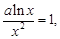 当
当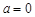 时,方程无解.当
时,方程无解.当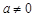 时,
时,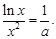
令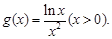 则
则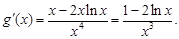 由
由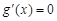 得
得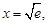
从而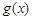 在
在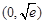 单调递增,在
单调递增,在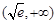 单调递减.
单调递减.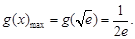
当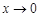 时,
时,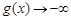 ,当
,当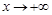
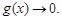
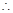 当
当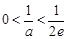 ,即
,即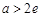 时,方程有两个不同解.
时,方程有两个不同解.
当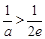 ,即
,即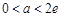 时,方程有0个解
时,方程有0个解
当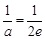 ,
,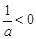 或即
或即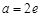 或
或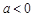 时,方程有唯一解.
时,方程有唯一解.
综上,当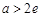 时,方程有两个不同解.当
时,方程有两个不同解.当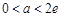 时,方程有0个解.当
时,方程有0个解.当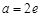 或
或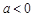 时,方程有唯一解. 9分.
时,方程有唯一解. 9分.
(3)特别地:当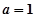 时由
时由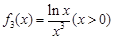 得
得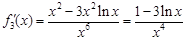 .
.
由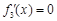 得
得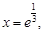
则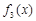 在
在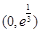 单调递增,在
单调递增,在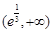 单调递减.
单调递减.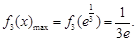
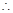
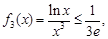 即
即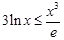 .又
.又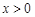 时,
时,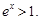
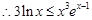 12分.
12分.
令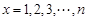 ,
,
则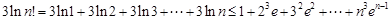 14分.
14分.
考点:1、导数的应用;2、不等式的证明.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 ,
,
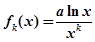 为
为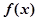 的
的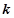 阶函数.
阶函数.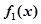 的单调区间;
的单调区间;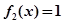 的解的个数;
的解的个数;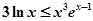 .
. 的函数
的函数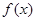 ,定义
,定义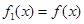 ,
,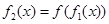 ,…,
,…,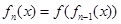 ,n=1,2,3,….满足
,n=1,2,3,….满足 的点称为f的
的点称为f的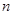 阶周期点.
阶周期点.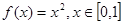 则f的
则f的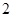 阶周期点的个数是___________;
阶周期点的个数是___________;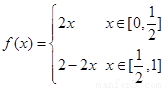 则f的
则f的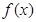 的图像在[a,b]上连续不断,定义:
的图像在[a,b]上连续不断,定义: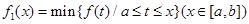 ,
, ,其中
,其中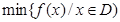 表示函数
表示函数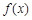 在D上的最小值,
在D上的最小值, 表示函数
表示函数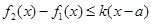 对任意的
对任意的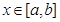 成立,则称函数
成立,则称函数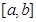 上的“k阶收缩函数”
上的“k阶收缩函数”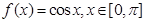 ,试写出
,试写出 ,
,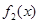 的表达式;
的表达式;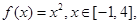 试判断
试判断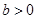 ,函数
,函数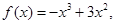 是[0,b]上的2阶收缩函数,求b的取值范围
是[0,b]上的2阶收缩函数,求b的取值范围 的图像在[a,b]上连续不断,定义:
的图像在[a,b]上连续不断,定义: ,
, ,其中
,其中 表示函数
表示函数 在D上的最小值,
在D上的最小值, 表示函数
表示函数 对任意的
对任意的 成立,则称函数
成立,则称函数 上的“k阶收缩函数”
上的“k阶收缩函数” ,试写出
,试写出 ,
, 的表达式;
的表达式; 试判断
试判断 ,函数
,函数 是[0,b]上的2阶收缩函数,求b的取值范围
是[0,b]上的2阶收缩函数,求b的取值范围