题目内容
设数列{an}的前n项和为Sn,且Sn=2an-2n+1.
(I)求证:( )是等差数列,并求出数列的{an}通项公式;
)是等差数列,并求出数列的{an}通项公式;
(II)数列{bn}满足bn=log2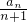 求使不等式(1+
求使不等式(1+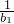 )(1+
)(1+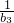 )…(1+
)…(1+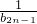 )≥m•
)≥m•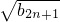 对任意正整数n都成立的最大实数m的值.
对任意正整数n都成立的最大实数m的值.
解:(Ⅰ)由Sn=2an-2n+1,得Sn-1=2an-1-2n(n≥2).
两式相减,得an=2an-2an-1-2n,即an-2an-1=2n (n≥2),(2分)
∴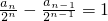 ,故数列{
,故数列{ }是公差为1的等差数列,(4分)
}是公差为1的等差数列,(4分)
又S1=2a1-22.则a1=4,∴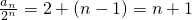 ,
,
故an=(n+1)+2n.(6分)
(Ⅱ)∵bn=log2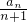 =
=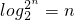 ,(7分)
,(7分)
不等式(1+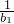 )(1+
)(1+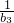 )…(1+
)…(1+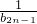 )≥m•
)≥m•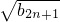 ,
,
即(1+1)(1+ )…(1+
)…(1+ )≥m•
)≥m• 恒成立,
恒成立,
也即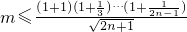 对任意正整数n都成立.(8分)
对任意正整数n都成立.(8分)
令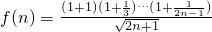 ,知
,知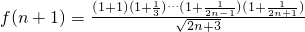 ,
,
∵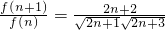 =
=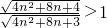 ,
,
∴当n∈N*时,f(n)单调递增,(10分)
∴f(n)≥f(1)= ,则m
,则m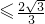 ,故实数m的最大值为
,故实数m的最大值为 .(12分)
.(12分)
分析:(Ⅰ)利用Sn=2an-2n+1,与Sn-1=2an-1-2n(n≥2).推出an-2an-1=2n (n≥2),然后证明数列{ }是公差为1的等差数列,即可求出数列的通项公式.
}是公差为1的等差数列,即可求出数列的通项公式.
(Ⅱ)利用bn=log2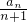 ,求出表达式,化简不等式(1+
,求出表达式,化简不等式(1+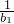 )(1+
)(1+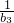 )…(1+
)…(1+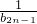 )≥m•
)≥m•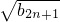 ,通过令
,通过令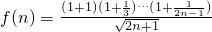 ,比较
,比较 的大小,说明f(n)单调递增,然后求出实数m的最大值.
的大小,说明f(n)单调递增,然后求出实数m的最大值.
点评:本题考查等差关系的确定,数列求和的应用,考查分析问题解决问题的能力,转化思想的应用.
两式相减,得an=2an-2an-1-2n,即an-2an-1=2n (n≥2),(2分)
∴
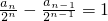 ,故数列{
,故数列{ }是公差为1的等差数列,(4分)
}是公差为1的等差数列,(4分)又S1=2a1-22.则a1=4,∴
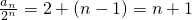 ,
,故an=(n+1)+2n.(6分)
(Ⅱ)∵bn=log2
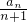 =
=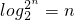 ,(7分)
,(7分)不等式(1+
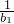 )(1+
)(1+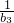 )…(1+
)…(1+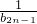 )≥m•
)≥m•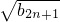 ,
,即(1+1)(1+
 )…(1+
)…(1+ )≥m•
)≥m• 恒成立,
恒成立,也即
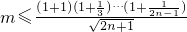 对任意正整数n都成立.(8分)
对任意正整数n都成立.(8分)令
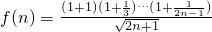 ,知
,知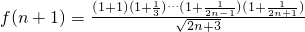 ,
,∵
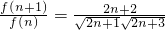 =
=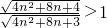 ,
,∴当n∈N*时,f(n)单调递增,(10分)
∴f(n)≥f(1)=
 ,则m
,则m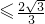 ,故实数m的最大值为
,故实数m的最大值为 .(12分)
.(12分)分析:(Ⅰ)利用Sn=2an-2n+1,与Sn-1=2an-1-2n(n≥2).推出an-2an-1=2n (n≥2),然后证明数列{
 }是公差为1的等差数列,即可求出数列的通项公式.
}是公差为1的等差数列,即可求出数列的通项公式.(Ⅱ)利用bn=log2
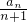 ,求出表达式,化简不等式(1+
,求出表达式,化简不等式(1+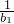 )(1+
)(1+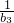 )…(1+
)…(1+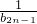 )≥m•
)≥m•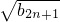 ,通过令
,通过令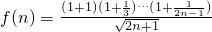 ,比较
,比较 的大小,说明f(n)单调递增,然后求出实数m的最大值.
的大小,说明f(n)单调递增,然后求出实数m的最大值.点评:本题考查等差关系的确定,数列求和的应用,考查分析问题解决问题的能力,转化思想的应用.

练习册系列答案
相关题目