题目内容
已知函数 ;
;
(1) 解不等式 ;
;
(2) 若对任意实数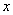 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1) (2)
(2)
解析试题分析:
(1)不等式
 即
即 ;
;
或  即解集为
即解集为 ; 或
; 或  即
即
综上:原不等式的解集为
解法二:作函数图象如下
不等式的解集为
(2)作函数 的图像如下:
的图像如下:
不等式 恒成立。 即
恒成立。 即 恒成立
恒成立
等价于函数 的图象恒在函数
的图象恒在函数 的图像上方,
的图像上方,
由图可知a的取值范围为 .
.
考点:绝对值不等式的解法 函数恒成立问题
点评:本题主要考查绝对值不等式的解法,函数的恒成立问题,属于中档题.

练习册系列答案
相关题目
 .
. 的不等式
的不等式 ;
;
 ,
, 恒成立,求
恒成立,求 的取值范围.
的取值范围.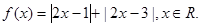 .
.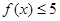 ;
;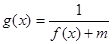 的定义域为
的定义域为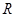 ,求实数
,求实数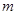 的取值范围.
的取值范围.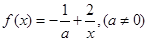 ,
,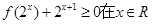 上恒成立,求a的取值范围。
上恒成立,求a的取值范围。  .
. 的不等式
的不等式 ;
;
 ,
, 恒成立,求
恒成立,求 的取值范围.
的取值范围. .
. 的不等式
的不等式 ;
;
 ,
, 恒成立,求
恒成立,求 的取值范围.
的取值范围.