题目内容
已知|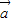 |=1,|
|=1,|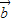 |=2,|
|=2,|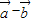 |=2,则|
|=2,则|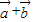 |= .
|= .
【答案】分析:根据平面向量模的运算性质,证出| |2+|
|2+| |2=2|
|2=2| |2+2|
|2+2| |2,由此代入题中的数据,可得|
|2,由此代入题中的数据,可得| |=
|= .
.
解答:解:∵| |2=|
|2=| |2-2
|2-2 •
• +|
+| |2,|
|2,| |2=|
|2=| |2+2
|2+2 •
• +|
+| |2,
|2,
∴| |2+|
|2+| |2=2|
|2=2| |2+2|
|2+2| |2,
|2,
∵| |=1,|
|=1,| |=2,|
|=2,| |=2
|=2
∴22+| |2=2×12+2×22,可得|
|2=2×12+2×22,可得| |2=6
|2=6
所以| |=
|=
故答案为:
点评:本题给出两个向量的模与它们差向量的模,求它们的和向量的模,着重考查了平面向量模的运算性质,属于基础题.
 |2+|
|2+| |2=2|
|2=2| |2+2|
|2+2| |2,由此代入题中的数据,可得|
|2,由此代入题中的数据,可得| |=
|= .
.解答:解:∵|
 |2=|
|2=| |2-2
|2-2 •
• +|
+| |2,|
|2,| |2=|
|2=| |2+2
|2+2 •
• +|
+| |2,
|2,∴|
 |2+|
|2+| |2=2|
|2=2| |2+2|
|2+2| |2,
|2,∵|
 |=1,|
|=1,| |=2,|
|=2,| |=2
|=2∴22+|
 |2=2×12+2×22,可得|
|2=2×12+2×22,可得| |2=6
|2=6所以|
 |=
|=
故答案为:

点评:本题给出两个向量的模与它们差向量的模,求它们的和向量的模,着重考查了平面向量模的运算性质,属于基础题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
已知
(xcosx+3a-b)dx=2a+6,f(t)=
(x3+ax+5a-b)dx为偶函数,则a+b=( )
| ∫ | 1 -1 |
| ∫ | t 0 |
| A、-6 | B、-12 | C、4 | D、-4 |