题目内容
已知a,b,c＞0，求证：aabbcc≥(abc)
.
思路分析：显然不等式两边为正，且是指数式，不妨设a≥b≥c，,则a-b,b-c,a-c∈R+,故尝试用作商比较法.
证明：等式关于a,b,c对称，不妨设a≥b≥c，则a-b,b-c,a-c∈R+，且,
，
都大于等于1.
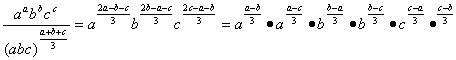
≥1.
∴aabbcc≥(abc)
.
练习册系列答案
阅读快车系列答案
相关题目
.阅读快车系列答案题目内容
已知a,b,c＞0，求证：aabbcc≥(abc).
思路分析：显然不等式两边为正，且是指数式，不妨设a≥b≥c，,则a-b,b-c,a-c∈R+,故尝试用作商比较法.
证明：等式关于a,b,c对称，不妨设a≥b≥c，则a-b,b-c,a-c∈R+，且,，都大于等于1.
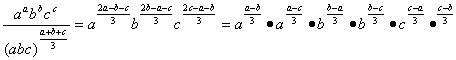
≥1.
∴aabbcc≥(abc).
阅读快车系列答案