题目内容
已知函数 (a为常数).
(a为常数).
(Ⅰ)求函数f(x)的最小正周期,并指出其单调减区间;
(Ⅱ)若函数f(x)在[0, ]上恰有两个x的值满足f(x)=2,试求实数a的取值范围.
]上恰有两个x的值满足f(x)=2,试求实数a的取值范围.
(本小题满分15分)
解:(Ⅰ)∵ =
= ,
,
∴最小正周期 ,
,
单调递减区间为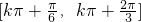 (k∈Z).
(k∈Z).
(Ⅱ)令 ,则
,则 ,
, .
.
要使g(u)在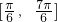 上恰有两个x的值满足g(u)=2,
上恰有两个x的值满足g(u)=2,
则 ,解得
,解得 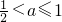 .
.
分析:(Ⅰ)通过二倍角公式以及两角和的正弦函数,化简函数为一个角的一个三角函数的形式,然后求出函数f(x)的最小正周期,通过正弦函数的单调减区间求出函数的单调减区间;
(Ⅱ)通过函数f(x)在[0, ]上恰有两个x的值满足f(x)=2,通过换元法,利用
]上恰有两个x的值满足f(x)=2,通过换元法,利用 ,试求实数a的取值范围.
,试求实数a的取值范围.
点评:本题考查三角函数的化简求值,二倍角公式与两角和的正弦函数的应用,函数的基本性质,考查计算能力.
解:(Ⅰ)∵
 =
= ,
,∴最小正周期
 ,
,单调递减区间为
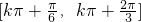 (k∈Z).
(k∈Z).(Ⅱ)令
 ,则
,则 ,
, .
.要使g(u)在
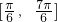 上恰有两个x的值满足g(u)=2,
上恰有两个x的值满足g(u)=2,则
 ,解得
,解得 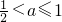 .
.分析:(Ⅰ)通过二倍角公式以及两角和的正弦函数,化简函数为一个角的一个三角函数的形式,然后求出函数f(x)的最小正周期,通过正弦函数的单调减区间求出函数的单调减区间;
(Ⅱ)通过函数f(x)在[0,
 ]上恰有两个x的值满足f(x)=2,通过换元法,利用
]上恰有两个x的值满足f(x)=2,通过换元法,利用 ,试求实数a的取值范围.
,试求实数a的取值范围.点评:本题考查三角函数的化简求值,二倍角公式与两角和的正弦函数的应用,函数的基本性质,考查计算能力.

练习册系列答案
 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 ( a为常数、a∈R),
( a为常数、a∈R), .
. (a为常数)的图象经过点(1,3).
(a为常数)的图象经过点(1,3). ( a为常数、a∈R),
( a为常数、a∈R), .
. (a为常数)是R上的奇函数,函数
(a为常数)是R上的奇函数,函数
 上恒成立,求t的取值范围
上恒成立,求t的取值范围 其中a为常数,且
其中a为常数,且 .
.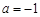 时,求
时,求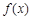 在
在 (e=2.718 28…)上的值域;
(e=2.718 28…)上的值域; 对任意
对任意 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.