题目内容
在函数f(x)=Asin(ωx+φ)(A>0,ω>0)的一个周期内,当x=| π |
| 9 |
| 1 |
| 2 |
| 4π |
| 9 |
| 1 |
| 2 |
| π |
| 2 |
分析:由最大值和最小值可求A,由相邻两个最大值与最小值之间相差半个周期可求ω,再通过函数f(x)=Asin(ωx+φ)过点(
,
)求φ.
| π |
| 9 |
| 1 |
| 2 |
解答:解:由最大值和最小值可知:A=
由当x=
时有最大值
,当x=
时有最小值-
可知其周期T=
∴ω=
=3
又∵函数f(x)=Asin(ωx+φ)过点(
,
)
∴
sin(
+∅) =
∵φ∈(0,
),
∴φ=
∴f(x)=
sin(3x+
)
故答案为:
sin(3x+
)
| 1 |
| 2 |
由当x=
| π |
| 9 |
| 1 |
| 2 |
| 4π |
| 9 |
| 1 |
| 2 |
| 2π |
| 3 |
∴ω=
| 2π |
| T |
又∵函数f(x)=Asin(ωx+φ)过点(
| π |
| 9 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
∵φ∈(0,
| π |
| 2 |
∴φ=
| π |
| 6 |
∴f(x)=
| 1 |
| 2 |
| π |
| 6 |
故答案为:
| 1 |
| 2 |
| π |
| 6 |
点评:本题主要考查三角函数中f(x)=Asin(ωx+φ)各参数的意义,A与最值有关,ω与周期有关,φ与点有关.

练习册系列答案
相关题目
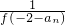 (n∈N*)
(n∈N*) (n∈N*)
(n∈N*) .
. 对不小于2的正整数恒成立,求x的取值范围.
对不小于2的正整数恒成立,求x的取值范围.