题目内容
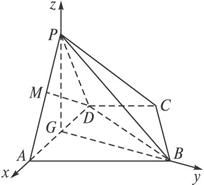
如图,四棱锥P—ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
(1)求证:AD⊥PB;
(2)求证:DM∥平面PCB;
(3)求二面角A-BC-P的正切值
解法一:(1)证明:取AD的中点G,连结PG、GB、BD.
∵PA=PD,∴PG⊥AD.
∵AB=AD,且∠DAB=60°,

∴△ABD是正三角形,BG⊥AD.
∴AD⊥平面PGB.
∴AD⊥PB.
(2)证明:取PB的中点F,连结MF、CF,
∵M、F分别为PA、PB的中点,
∴MF∥AB,且MF=![]() AB.
AB.
∵四边形ABCD是直角梯形,AB∥CD且AB=2CD,
∴MF∥CD且MF=CD.
∴四边形CDFM是平行四边形.
∴DM∥CF.
∵CF![]() 平面PCB,
平面PCB,
∴DM∥平面PCB.
(3)取BC的中点E,连结PE、GE.
∵四边形ABCD是直角梯形且AB∥CD,
∴GE∥AB,GE⊥BC.
∴BC⊥平面PEG.
∴BC⊥PE.
∴∠PEG是二面角ABCP的平面角.
设DC=a,则AB=AD=2a.
∵G、E分别为AD、BC中点,
∴GE=![]() =
=![]() =
=![]() a.
a.
∵G是等腰直角三角形PAD斜边的中点,
∴PG=![]() AD=a.13分
AD=a.13分
∴tan∠PEG=![]() =
=![]() .
.
∴二面角ABCP的正切值为![]() .
.
解法二:(1)同解法一.
(2)证明:∵侧面PAD⊥底面ABCD,
又∵PG⊥AD,∴PG⊥底面ABCD.
∴PG⊥BG.
∵PG⊥AD,
∴直线AD、GB、GP两两互相垂直,故可以分别以直线AD、GB、GP为x轴、y轴和z轴建立如图所示的空间直角坐标系G—xyz.
设PG=a,C(x,y,z),则可求得P(0,0,a),A(a,0,0),B(0,![]() a,0),D(-a,0,0),则
a,0),D(-a,0,0),则
![]() =(0,0,a),
=(0,0,a),![]() =(-a,
=(-a,![]() a,0),
a,0),![]() =(0,
=(0,![]() a,-a).
a,-a).
∵AB=2DC且AB∥CD,∴![]() =2
=2![]() ,
,
即(-a,![]() a,0)=2[(x,y,z)-(-a,0,0)].
a,0)=2[(x,y,z)-(-a,0,0)].
∴(x,y,z)=(![]() a,
a,![]() a,0),即C(
a,0),即C(![]() a,
a,![]() a,0).∴BC=(
a,0).∴BC=(![]() a,
a,![]() a,0).
a,0).
设n=(x0,y0,z0)是平面PBC的法向量,则n·![]() =0且n·
=0且n·![]() =0.
=0.
∴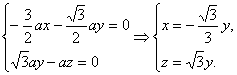
取y=![]() ,得n=(-1,
,得n=(-1,![]() ,3).∵M是AP的中点,∴M(
,3).∵M是AP的中点,∴M(![]() ,0,
,0,![]() ).
).
∴![]() =(
=(![]() ,0,
,0,![]() )-(-a,0,0)=(
)-(-a,0,0)=(![]() a,0,
a,0,![]() ).
).
![]() ·n=(
·n=(![]() a,0,
a,0,![]() )·(-1,
)·(-1,![]() ,3)=0.
,3)=0.
∴![]() ⊥n.∵
⊥n.∵![]()
![]() 平面PCB,∴DM∥平面PCB.
平面PCB,∴DM∥平面PCB.
(3)∵PG⊥平面ABCD,∴GP是平面ABCD的法向量.
∴cos〈n,![]() 〉=
〉=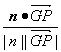 =
=![]() .
.
∴tan〈n,![]() 〉=
〉=![]() .∴二面角A-BC-P的正切值为
.∴二面角A-BC-P的正切值为![]() .
.

 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=