题目内容
【题目】为迎接春节,某工厂大批生产小孩具—— 拼图,工厂为了规定工时定额,需要确定加工拼图所花费的时间,为此进行了10次试验,测得的数据如下:
拼图数
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
加工时间
| 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
(1)画出散点图,并判断![]() 与
与![]() 是否具有线性相关关系;
是否具有线性相关关系;

(2)求回归方程;
(3)根据求出的回归方程,预测加工2010个拼图需要用多少小时?(精确到0.1)
附:回归直线的斜率和截距的最小二乘估计公式分别为:
 ,
, ![]() .
.
参考数据 | 合计 | ||||||||||
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 550 |
| 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 | 917 |
| 100 | 400 | 900 | 1600 | 2500 | 3600 | 4900 | 6400 | 8100 | 10000 | 38500 |
| 620 | 1360 | 2250 | 3240 | 4450 | 5700 | 7140 | 8840 | 10350 | 12200 | 55950 |
【答案】(1)见解析;(2)![]() ;(3)加工2010个拼图所需时间约为23.3小时.
;(3)加工2010个拼图所需时间约为23.3小时.
【解析】试题分析:(1)根据表中数据,画出散点图,
由散点图成带状分布,得出两个变量具有线性相关关系;
(2)计算![]() ,求出回归系数
,求出回归系数![]() ,写出回归方程;
,写出回归方程;
(3)计算x=200时![]() 的值即可.
的值即可.
试题解析:
(1)散点图如图所示,
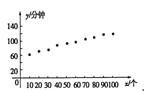
由散点图可以看出,两个变量具有线性相关关系.
(2)经计算得![]() ,
, ![]() ,求和
,求和![]() ,求和
,求和![]() ,
,
设所求的回归方程为![]() ,则有
,则有![]() ,
, ![]() ,
,
因此,所求的回归方程是![]() .
.
(3)当![]() 时,
时, ![]() (分钟),
(分钟),![]() ,
,
因此,加工2010个拼图所需时间约为23.3小时.

【题目】为贯彻落实教育部等![]() 部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,普及足球知识和技能,市教体局决定举行春季校园足球联赛,为迎接此次联赛,甲中学选拔了
部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,普及足球知识和技能,市教体局决定举行春季校园足球联赛,为迎接此次联赛,甲中学选拔了![]() 名学生组成集训队,现统计了这
名学生组成集训队,现统计了这![]() 名学生的身高,记录如下表:
名学生的身高,记录如下表:
身高 |
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
(1)请计算这![]() 名学生的身高中位数、众数,并补充完成下面的茎叶图:
名学生的身高中位数、众数,并补充完成下面的茎叶图:

(2)身高为![]() 和
和![]() 的四名学生分别为
的四名学生分别为![]() ,现从这四名学生中选
,现从这四名学生中选![]() 名担任正副门将,请利用列举法列出所有可能情况,并求学生
名担任正副门将,请利用列举法列出所有可能情况,并求学生![]() 入选正门将的概率.
入选正门将的概率.
【题目】为了弘扬民族文化,某校举行了“我爱国学,传诵经典”考试,并从中随机抽取了100名考生的成绩(得分均为整数,满分100分)进行统计制表,其中成绩不低于80分的考生被评为优秀生,请根据频率分布表中所提供的数据,用频率估计概率,回答下列问题.
分组 | 频数 | 频率 |
| 5 |
|
|
|
|
| 35 |
|
| 25 |
|
| 15 |
|
合计 | 100 |
|
(Ⅰ)求![]() 的值及随机抽取一考生恰为优秀生的概率;
的值及随机抽取一考生恰为优秀生的概率;
(Ⅱ)按成绩采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;
(Ⅲ)在第(Ⅱ)问抽取的优秀生中指派2名学生担任负责人,求至少一人的成绩在![]() 的概率.
的概率.


