题目内容
设函数f（x）是定义在R上的以7为周期的奇函数，若f （5）＞1，f （2011）=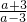
，则a的取值范围是
- A.（-∞，0）
- B.（0，3）
- C.（0，+∞）
- D.（-∞，0）∪（3，+∞）
B
分析：利用函数的周期性和奇偶性，将f （2011）转化为f（5）的关系，然后利用f （5）＞1，解不等式即可．
解答：因为函数f（x）的周期是7，所以f （2011）=f （288×7-5）=f （-5），
因为函数为奇函数，所以f （2011）=f （288×7-5）=f （-5）=-f（5），
因为f （2011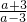）=，f （5）＞1，所以f （2011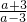）==-f （5）＜-1，
即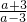+1＜0，所以
，解得0＜a＜3．
故选B．
点评：本题主要考查函数奇偶性和周期性的应用．
分析：利用函数的周期性和奇偶性，将f （2011）转化为f（5）的关系，然后利用f （5）＞1，解不等式即可．
解答：因为函数f（x）的周期是7，所以f （2011）=f （288×7-5）=f （-5），
因为函数为奇函数，所以f （2011）=f （288×7-5）=f （-5）=-f（5），
因为f （2011）=
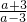，f （5）＞1，所以f （2011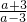）==-f （5）＜-1，即
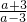+1＜0，所以，解得0＜a＜3．故选B．
点评：本题主要考查函数奇偶性和周期性的应用．
练习册系列答案
相关题目