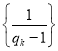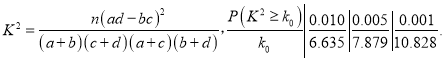题目内容
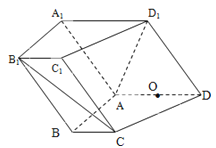
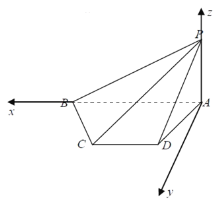
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() .
.
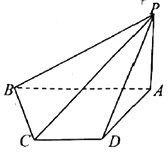
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 夹角的余弦值,
夹角的余弦值,
【答案】(1)见解析;(2)![]()
【解析】
(1)结合题中数据在四边形![]() 中证得
中证得![]() ,由平面
,由平面![]() 面
面![]() ,得
,得![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() ,可得
,可得![]() 平面
平面![]() ;(2)以
;(2)以![]() 坐标原点,分别以
坐标原点,分别以![]()
![]() 在的直线为
在的直线为![]() 、
、![]() 轴,在底面
轴,在底面![]() 内点过点
内点过点![]() 作
作![]() 垂线为
垂线为![]() 轴建立空间直角坐标系,写出各点坐标,分别求出平面
轴建立空间直角坐标系,写出各点坐标,分别求出平面![]() 与平面
与平面![]() 的法向量,然后计算其夹角,由二面角的平面角与法向量的关系得到答案.
的法向量,然后计算其夹角,由二面角的平面角与法向量的关系得到答案.
解(1)![]() ,
,![]() ,
,![]() .
.
![]() ,根据勾股定理可知
,根据勾股定理可知![]() .
.
又![]() 平面
平面![]() 面
面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.![]() .
.
又![]() ,
,![]() 平面
平面![]() .
.
(2)以![]() 坐标原点,分别以
坐标原点,分别以![]()
![]() 在的直线为
在的直线为![]() 、
、![]() 轴,在底面
轴,在底面![]() 内点过点
内点过点![]() 作
作![]() 垂线为
垂线为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则![]() ,
,![]() ,
,![]() ,
,![]()
所以![]() ,
,![]() ,
,![]()
设平面![]() 法向量为
法向量为![]() ,
,
则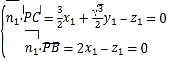 ,
,
取![]() ,
,![]() ,
,![]()
![]() 平面
平面![]() 一个法向量为
一个法向量为![]() ,
,
设平面![]() 法向量为
法向量为![]() ,
,
则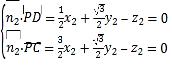 ,
,
取![]() ,
,![]() ,
,![]()
![]() 平面
平面![]() 一个法向量为
一个法向量为![]() ,
,
![]()
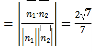
由图易知平面![]() 与平面
与平面![]() 夹角为锐角
夹角为锐角
所以平面 ![]() 平面
平面![]() 成夹角的余弦值为
成夹角的余弦值为![]() .
.

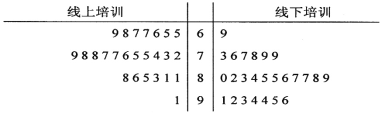
【题目】袋子中有四张卡片,分别写有“瓷、都、文、明”四个字,有放回地从中任取一张卡片,将三次抽取后“瓷”“都”两个字都取到记为事件![]() ,用随机模拟的方法估计事件
,用随机模拟的方法估计事件![]() 发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
232 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估计事件![]() 发生的概率为( )
发生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
,![]()