题目内容
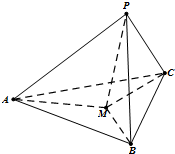
如图,在三棱锥P—ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
(1)求证OD∥平面PAB;
(2)当k=
时,求直线PA与平面PBC所成角的大小;
(3)当k取何值时,O在平面PBC内的射影恰好为△PBC的重心?
(1)证明:∵O、D分别为AC、PC的中点,
∴OD∥PA.
又PA平面PAB,
∴OD∥平面PAB.
(2)解:∵AB⊥BC,OA=OC,∴OA=OB=OC.
又∵OP⊥平面ABC,∴PA=PB=PC.
取BC中点E,连结PE,则BC⊥平面POE.
作OF⊥PE于F,连结DF,则OF⊥平面PBC,
∴∠ODF是OD与平面PBC所成的角.
又OD∥PA,∴PA与平面PBC所成角的大小等于∠ODF.
在Rt△ODF中,sin∠ODF=
,
∴PA与平面PBC所成的角为arcsin
.
(3)解:由(2)知OF⊥平面PBC,∴F是O在平面PBC内的射影.
∵D是PC的中点,若点F是△PBC的重心,则B、F、D三点共线.
∴直线OB在平面PBC内的射影为直线BD.
∵OB⊥PC,∴PC⊥BD.
∴PB=BC,即k=1.
反之,当k=1时,三棱锥O—PBC为正三棱锥,
∴O在平面PBC内的射影为△PBC的重心.
练习册系列答案
阅读快车系列答案
相关题目
如图，在三棱锥P-ABC中，PA、PB、PC两两垂直，且PA=3．PB=2，PC=1．设M是底面ABC内一点，定义f（M）=（m，n，p），其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积．若f（M）=（
如图，在三棱锥P-ABC中，PA⊥底面ABC，∠ACB=90°，AE⊥PB于E，AF⊥PC于F，若PA=AB=2，∠BPC=θ，则当△AEF的面积最大时，tanθ的值为（ ）
如图，在三棱锥P-ABC中，PA=PB=AB=2，BC=3，∠ABC=90°，平面PAB⊥平面ABC，D、E分别为AB、AC中点．
如图，在三棱锥P-ABC中，已知PA=PB=PC，∠BPA=∠BPC=∠CPA=40°，一绳子从A点绕三棱锥侧面一圈回到点A的最短距离是
如图，在三棱锥P-ABC中，PA⊥底面ABC，∠BCA=90°，AP=AC，点D，E分别在棱