题目内容
在平面直角坐标系xOy中,若动点P(a,b)到两直线l1:y=x和l2:y=-x+2的距离之和为2
,则a2+b2的最大值为 .
| 2 |
分析:利用点到直线的距离公式可得:|a-b|+|a+b-2|=4.通过分类讨论可知:点(a,b)是如图所示的正方形的4条边.即可得到
最大值.
| a2+b2 |
解答:解:∵动点P(a,b)到两直线l1:y=x和l2:y=-x+2的距离之和为2
,
∴
+
=2
,
化为|a-b|+|a+b-2|=4.
分为以下4种情况:
或
或
或
.
可知点(a,b)是如图所示的正方形的4条边.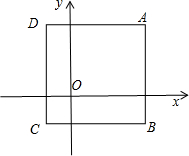
可知:当取点A时,
取得最大值
=
.
∴a2+b2的最大值为18.
故答案为:18.
| 2 |
∴
| |a-b| | ||
|
| |a+b-2| | ||
|
| 2 |
化为|a-b|+|a+b-2|=4.
分为以下4种情况:
|
|
|
|
可知点(a,b)是如图所示的正方形的4条边.

可知:当取点A时,
| a2+b2 |
| 32+32 |
| 18 |
∴a2+b2的最大值为18.
故答案为:18.
点评:本题考查了点到直线的距离公式、含绝对值的等式、分类讨论等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是