题目内容
已知椭圆C: (a>b≥0),其离心率为
(a>b≥0),其离心率为 ,两准线之间的距离为
,两准线之间的距离为 .
.
(1)求a,b之值;
(2)设点A坐标为(6,0),B为椭圆C上的动点,以A为直角顶点,作等腰直角△ABP(字母A,B,P按顺时针方向排列),求P点的轨迹方程.
解:(1)设c为椭圆的焦半径,则 ,于是有a=5,c=4,∴b=3.
,于是有a=5,c=4,∴b=3.
(2)解法一:设B点坐标为(s,t),P点坐标为(x,y).
于是有 .
.
因为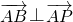 ,所以有(s-6,t)(x-6,y)=(s-6)(x-6)+ty=0. ①
,所以有(s-6,t)(x-6,y)=(s-6)(x-6)+ty=0. ①
又因为△ABP为等腰直角三角形,所以有|AB|=|AP|,即 . ②
. ②
由①推出 ,代入②得t2=(x-6)2
,代入②得t2=(x-6)2
从而有 y2=(s-6)2,即s=6+y(不合题意,舍去)或s=6-y.
代入椭圆方程,即得动点P的轨迹方程 .
.
解法二:设B(x1,y1),P(x,y),|AB|=r,则以A为圆心,r为半径的圆的参数方程为 .
.
设AB与x轴正方向夹角为θ,B点的参数表示为 ,
,
P点的参数表示为 ,即
,即 .
.
从上面两式,得到 .
.
又由于B点在椭圆上,可得 .
.
此即为P点的轨迹方程.
分析:(1)根据椭圆C: (a>b≥0),其离心率为
(a>b≥0),其离心率为 ,两准线之间的距离为
,两准线之间的距离为 ,我们可以得到几何量之间的关系,由此可以求a,b之值;
,我们可以得到几何量之间的关系,由此可以求a,b之值;
(2)解法一:利用等腰直角△ABP条件,寻找B与P坐标之间的关系,利用B为椭圆C上的动点,可求动点P的轨迹方程;
解法二:利用圆的参数方程,寻找B与P坐标之间的关系,利用B为椭圆C上的动点,可求动点P的轨迹方程.
点评:椭圆的性质的灵活运用,是我们思路的关键,利用代入法求解两动点的轨迹问题,是我们解决这类问题的常用方法.
 ,于是有a=5,c=4,∴b=3.
,于是有a=5,c=4,∴b=3.(2)解法一:设B点坐标为(s,t),P点坐标为(x,y).
于是有
 .
.因为
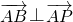 ,所以有(s-6,t)(x-6,y)=(s-6)(x-6)+ty=0. ①
,所以有(s-6,t)(x-6,y)=(s-6)(x-6)+ty=0. ①又因为△ABP为等腰直角三角形,所以有|AB|=|AP|,即
 . ②
. ②由①推出
 ,代入②得t2=(x-6)2
,代入②得t2=(x-6)2从而有 y2=(s-6)2,即s=6+y(不合题意,舍去)或s=6-y.
代入椭圆方程,即得动点P的轨迹方程
 .
.解法二:设B(x1,y1),P(x,y),|AB|=r,则以A为圆心,r为半径的圆的参数方程为
 .
.设AB与x轴正方向夹角为θ,B点的参数表示为
 ,
,P点的参数表示为
 ,即
,即 .
.从上面两式,得到
 .
.又由于B点在椭圆上,可得
 .
.此即为P点的轨迹方程.
分析:(1)根据椭圆C:
 (a>b≥0),其离心率为
(a>b≥0),其离心率为 ,两准线之间的距离为
,两准线之间的距离为 ,我们可以得到几何量之间的关系,由此可以求a,b之值;
,我们可以得到几何量之间的关系,由此可以求a,b之值;(2)解法一:利用等腰直角△ABP条件,寻找B与P坐标之间的关系,利用B为椭圆C上的动点,可求动点P的轨迹方程;
解法二:利用圆的参数方程,寻找B与P坐标之间的关系,利用B为椭圆C上的动点,可求动点P的轨迹方程.
点评:椭圆的性质的灵活运用,是我们思路的关键,利用代入法求解两动点的轨迹问题,是我们解决这类问题的常用方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
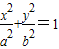 (a>b>0)的左、右焦点分别为F1(-1,0)、F2(1,0),离心率为
(a>b>0)的左、右焦点分别为F1(-1,0)、F2(1,0),离心率为 .
. (O为坐标原点),求△AOB的面积;
(O为坐标原点),求△AOB的面积;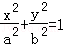 (a>b>0)的两个焦点分别为F1(﹣1,0),F2(1,0),且椭圆C经过点
(a>b>0)的两个焦点分别为F1(﹣1,0),F2(1,0),且椭圆C经过点 .
. ,求点Q的轨迹方程.
,求点Q的轨迹方程. (a>b>0)的一个顶点为A(2,0),离心率为
(a>b>0)的一个顶点为A(2,0),离心率为 ,直线y=k(x-1)与椭圆C交于不同的两点M、N.
,直线y=k(x-1)与椭圆C交于不同的两点M、N. 时,求k的值.
时,求k的值. +
+ =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+ 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同两点A,B且线段AB的垂直平分线过定点C(
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同两点A,B且线段AB的垂直平分线过定点C( ,0)求实数k的取值范围。
,0)求实数k的取值范围。 (a>b>0)的离心率为
(a>b>0)的离心率为 ,过右焦点F且斜率为k(k>0)的直线与椭圆C相交于A、B两点,若
,过右焦点F且斜率为k(k>0)的直线与椭圆C相交于A、B两点,若 。则
。则 ( )
( )  (D)
(D)