题目内容
△ABC中,角A,B,C所对的边分别是a,b,c,且cosA= .
.(1)求
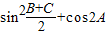 的值;
的值;(2)若b=2,△ABC的面积S=3,求a的值.
【答案】分析:(1)利用诱导公式及二倍角的余弦公式对式子化简,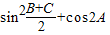 =
=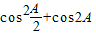 =
=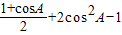 ,代入可求
,代入可求
(2)由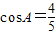 可求sinA,代入三角形的面积公式 S=
可求sinA,代入三角形的面积公式 S=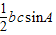 可求c,然后利用余弦定理可得a2=b2+c2-2bccosA可求a
可求c,然后利用余弦定理可得a2=b2+c2-2bccosA可求a
解答:解:(1)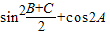 =
=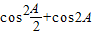
=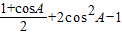
=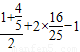 =
=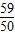 (6分)
(6分)
(2)∵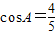 ∴
∴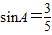 S=
S=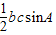 =
=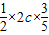 =3
=3
∴c=5,a2=b2+c2-2bccosA=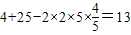
∴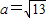 (7分)
(7分)
点评:本题主要考查了三角函数的诱导公式及二倍角公式、同角平分关系及余弦定理在三角函数求值化简中的应用.
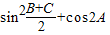 =
=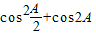 =
=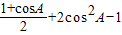 ,代入可求
,代入可求(2)由
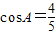 可求sinA,代入三角形的面积公式 S=
可求sinA,代入三角形的面积公式 S=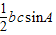 可求c,然后利用余弦定理可得a2=b2+c2-2bccosA可求a
可求c,然后利用余弦定理可得a2=b2+c2-2bccosA可求a解答:解:(1)
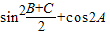 =
=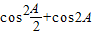
=
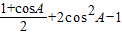
=
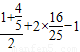 =
=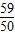 (6分)
(6分)(2)∵
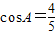 ∴
∴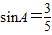 S=
S=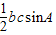 =
=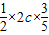 =3
=3 ∴c=5,a2=b2+c2-2bccosA=
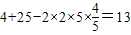
∴
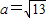 (7分)
(7分)点评:本题主要考查了三角函数的诱导公式及二倍角公式、同角平分关系及余弦定理在三角函数求值化简中的应用.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目