题目内容
已知![]() ,函数
,函数![]() ,
,![]() .
.
(1)求函数![]() 在区间
在区间![]() 上的最小值;
上的最小值;
(2)是否存在实数![]() ,使曲线
,使曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直?若存在,求出
轴垂直?若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)求证:![]() .
.
解:(1)函数![]() 的定义域为
的定义域为![]()
∵ ![]() ∴
∴ ![]()
令 ![]()
若![]() ,则
,则![]() ,
,![]() 在区间
在区间![]() 上单调递增,此时,
上单调递增,此时,![]() 无最小值;
无最小值;
② 若![]() ,则当
,则当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
∴当![]() 时,
时,![]() 有最小值
有最小值![]() ;
;
③ 若![]() ,则
,则![]() ,
,![]() 在区间
在区间![]() 上单调递减,
上单调递减,
∴当![]() 时,
时,![]() 有最小值
有最小值![]() .
.
综上:
(2) ∵ ![]() ∴
∴ ![]()
由(1)可知:当![]() 时,
时,![]() 在区间
在区间![]() 上有最小值
上有最小值![]()
∴![]()
∴当![]() 时,
时,![]()
∵曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直等价于:方程
轴垂直等价于:方程![]() 有实数解,而
有实数解,而 ![]() 即方程
即方程![]() 无实数解,故不存在实数
无实数解,故不存在实数![]() ,使曲线
,使曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直.
轴垂直.
(3)(理)由(1)可知:当![]() 时,
时,![]() 对
对![]() 恒成立,
恒成立,
即 当![]() 时,恒有
时,恒有![]() ........(*)
........(*)
取![]() ,得
,得![]()
∴![]()
故 ![]()
又 在(*)式中,取![]() ,得:
,得:
![]()
∴ ![]()
故 ![]()
或:又 在(*)式中,取![]() ,得:
,得:![]()
∴ ![]()
故 ![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 ,函数
,函数 的
的 .
. .
.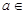 R,函数
R,函数 (x∈R).
(x∈R).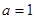 时,求函数f(x)的单调递增区间;
时,求函数f(x)的单调递增区间;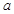 的取值范围;若不能,请说明理由;
的取值范围;若不能,请说明理由;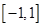 上单调递增,求
上单调递增,求