题目内容
已知函数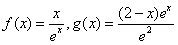 ,
,
(1)求函数f(x)的极值;
(2)求证:当x>1时,f(x)>g(x);
(3)如果x1<x2,且f(x1)=f(x2),求证:f(x1)>f(2-x2)。
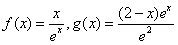 ,
, (1)求函数f(x)的极值;
(2)求证:当x>1时,f(x)>g(x);
(3)如果x1<x2,且f(x1)=f(x2),求证:f(x1)>f(2-x2)。
(1)解:∵ ,∴
,∴ ,
,
令f′(x)=0,解得x=1,
f(x)、f′(x)随x的变化情况见下表:

∴当x=1时,f(x)取得极大值f(1)= ;
;
(2)证明:令 ,
,
则 ,
,
当x>1时,1-x<0,2x>2,从而 <0,
<0,
∴ >0,F(x)在(1,+∞)是增函数,
>0,F(x)在(1,+∞)是增函数,
∴ ,
,
故当x>1时,f(x)>g(x)。
(3)证明:∵f(x)在(-∞,1)内是增函数,在(1,+∞)内是减函数,
∴当 ,且
,且 时,x1、x2不可能在同一单调区间内,
时,x1、x2不可能在同一单调区间内,
∴ ,
,
由(2)的结论知x>1时, >0,
>0,
∴ ,
,
∵ ,
,
∴ ,
,
又 ,
,
∴ 。
。
 ,∴
,∴ ,
,令f′(x)=0,解得x=1,
f(x)、f′(x)随x的变化情况见下表:

∴当x=1时,f(x)取得极大值f(1)=
 ;
; (2)证明:令
 ,
,则
 ,
,当x>1时,1-x<0,2x>2,从而
 <0,
<0,∴
 >0,F(x)在(1,+∞)是增函数,
>0,F(x)在(1,+∞)是增函数, ∴
 ,
,故当x>1时,f(x)>g(x)。
(3)证明:∵f(x)在(-∞,1)内是增函数,在(1,+∞)内是减函数,
∴当
 ,且
,且 时,x1、x2不可能在同一单调区间内,
时,x1、x2不可能在同一单调区间内,∴
 ,
,由(2)的结论知x>1时,
 >0,
>0,∴
 ,
, ∵
 ,
,∴
 ,
,又
 ,
,∴
 。
。 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. 的单调区间;
的单调区间; ,
, 在区间
在区间 恒成立,求a的取值范围.
恒成立,求a的取值范围. ,
,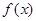 的单调递减区间;
的单调递减区间; 时,求函数
时,求函数 .
. .
. 的单调区间;
的单调区间; 时,判断
时,判断 和
和 的大小,并说明理由;
的大小,并说明理由; 时,关于
时,关于 的方程:
的方程: 在区间
在区间 上总有两个不同的解.
上总有两个不同的解. ,
,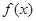 的最小值;
的最小值; 都有
都有 ,求实数
,求实数 的取值范围.
的取值范围.