Question

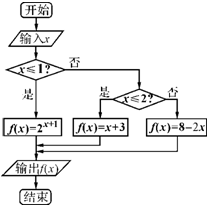已知x∈R，根据右图所示的程序框图，则不等式f(x)≥-

1

2

x+2的解集是

 

．

Answer 1

分析：根据题中所给的程序框图，可知该程序的功能是计算一个分段函数，将分段函数的解析式表示出来，进行分类求解不等式f(x)≥-

1

2

x+2的解集，从而得到答案．

解答：解：根据程序框图可知，该程序的功能为计算f（x）=

2x+1，x≤1 x+3，1＜x≤2 8-2x，x＞2

，
∵不等式f(x)≥-

1

2

x+2，
①当x≤1时，f（x）=2^x+1，
故不等式即为2^x+1≥-

1

2

x+2，即2^x+1+

1

2

x-2≥0，
令g（x）=2^x+1+

1

2

x-2，则g′（x）=2^x+1+

1

2

＞0恒成立，
∴g（x）=2^x+1+

1

2

x-2在（-∞，1]上单调递增，
∵g（0）=0，
又∵g（x）≥0，
∴x≥0，且x≤1，即0≤x≤1，
故不等式f(x)≥-

1

2

x+2的解集为{x|0≤x≤1}；
②当1＜x≤2时，f（x）=x+3，
故不等式即为x+3≥-

1

2

x+2，
解得x≤-

2

3

，
又∵1＜x≤2，
故不等式f(x)≥-

1

2

x+2的解集为∅；
③当x＞2时，f（x）=8-2x，
故不等式即为8-2x≥-

1

2

x+2，
解得x≤4，
故不等式f(x)≥-

1

2

x+2的解集为{x|2＜x≤4}．
综合①②③可得，不等式f(x)≥-

1

2

x+2的解集为[0，4]．
故答案为：[0，4]．

点评：本题考查了程序框图，分段函数问题．程序框图中对应的知识点是条件结构，其中正确理解各变量的含义并根据程序功能的需要合理的分析是解答的关键．考查了分段函数的解不等式，该题是分段函数故需讨论用哪段解析式，同时考查了利用函数单调性解不等式．属于基础题．