题目内容
设T= .
.(1)已知sin(π-θ )=
 ,θ为钝角,求T的值;
,θ为钝角,求T的值;(2)已知 cos(
 -θ )=m,θ 为钝角,求T的值.
-θ )=m,θ 为钝角,求T的值.
【答案】分析:(1)由条件求出sinθ和cosθ 的值,代入T= =
=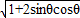 进行运算.
进行运算.
(2)利用诱导公式、同角三角函数的基本关系求出sinθ和cosθ 的值,由T=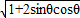 =|sinθ+cosθ|,分类讨论去掉绝对值求得T值.
=|sinθ+cosθ|,分类讨论去掉绝对值求得T值.
解答:解:(1)由sin(π-θ)= ,得 sinθ=
,得 sinθ= ,∵θ 为钝角,∴cosθ=-
,∵θ 为钝角,∴cosθ=- ,
,
∴sin2θ=2sinθcosθ= ,T=
,T= =
= .
.
(2)由 ,∵θ为钝角,∴
,∵θ为钝角,∴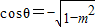 ,
,
T=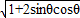 =|sinθ+cosθ|,∵
=|sinθ+cosθ|,∵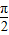 <θ<π,∴当
<θ<π,∴当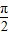 <θ<
<θ<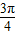 时,sinθ+cosθ>0,
时,sinθ+cosθ>0,
∴T=sinθ+cosθ=m- ,
,
∴当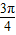 <θ<π 时,sinθ+cosθ<0,∴T=-(sinθ+cosθ )=-m+
<θ<π 时,sinθ+cosθ<0,∴T=-(sinθ+cosθ )=-m+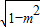 .
.
点评:本题考查同角三角函数的基本关系,诱导公式的应用,体现了分类讨论的数学思想,确定三角函数值的符号是解题的难点.
 =
=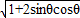 进行运算.
进行运算.(2)利用诱导公式、同角三角函数的基本关系求出sinθ和cosθ 的值,由T=
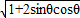 =|sinθ+cosθ|,分类讨论去掉绝对值求得T值.
=|sinθ+cosθ|,分类讨论去掉绝对值求得T值.解答:解:(1)由sin(π-θ)=
 ,得 sinθ=
,得 sinθ= ,∵θ 为钝角,∴cosθ=-
,∵θ 为钝角,∴cosθ=- ,
,∴sin2θ=2sinθcosθ=
 ,T=
,T= =
= .
.(2)由
 ,∵θ为钝角,∴
,∵θ为钝角,∴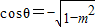 ,
,T=
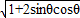 =|sinθ+cosθ|,∵
=|sinθ+cosθ|,∵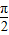 <θ<π,∴当
<θ<π,∴当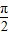 <θ<
<θ<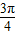 时,sinθ+cosθ>0,
时,sinθ+cosθ>0,∴T=sinθ+cosθ=m-
 ,
,∴当
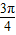 <θ<π 时,sinθ+cosθ<0,∴T=-(sinθ+cosθ )=-m+
<θ<π 时,sinθ+cosθ<0,∴T=-(sinθ+cosθ )=-m+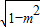 .
.点评:本题考查同角三角函数的基本关系,诱导公式的应用,体现了分类讨论的数学思想,确定三角函数值的符号是解题的难点.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目