题目内容
函数f（x）与的图象与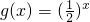
图象关于直线y=x对称，则的f（4-x2）的单调增区间是
- A.（-∞，0]
- B.[0，+∞）
- C.（-2，0]
- D.[0，2）
D
分析：函数f（x）是g（x）=
的反函数，求出f（4-x2）的解析式，确定单调减区间．
解答：∵函数f（x）与g（x）=的图象关于直线y=x对称，
∴函数f（x）是g（x）=的反函数，∴f（x）=
，
f（4-x2）=
又 4-x2＞0，-2＜x＜2，
∴f（4-x2）的增区间[0，2）
故选D．
点评：本题考查反函数，函数的单调性和单调区间．
分析：函数f（x）是g（x）=
的反函数，求出f（4-x2）的解析式，确定单调减区间．解答：∵函数f（x）与g（x）=
的图象关于直线y=x对称，∴函数f（x）是g（x）=
的反函数，∴f（x）=，f（4-x2）=
又 4-x2＞0，-2＜x＜2，∴f（4-x2）的增区间[0，2）
故选D．
点评：本题考查反函数，函数的单调性和单调区间．
练习册系列答案
相关题目
函数f（x）与的图象与g(x)=(
)x图象关于直线y=x对称，则的f（4-x2）的单调增区间是（ ）
| 1 |
| 2 |
| A、（-∞，0] |
| B、[0，+∞） |
| C、（-2，0] |
| D、[0，2） |
图象关于直线y=x对称，则的f（4-x2）的单调增区间是（ ）
图象关于直线y=x对称，则的f（4-x2）的单调增区间是（ ）
图象关于直线y=x对称，则的f（4-x2）的单调增区间是（ ）
．
的图象总在直线y=a的上方，求实数a的取值范围；
的图象有公共点，且在公共点处的切线相同，求实数m的值．